
【题目】如图,已知反比例函数y1=![]() (k1﹥0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.
(k1﹥0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.

(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
【答案】(1)、y=x+1;y=![]() ;(2)、0<x<1和x<-2.
;(2)、0<x<1和x<-2.
【解析】
试题分析:(1)、首先设OC=m,根据tan∠AOC的大小求出AC的值,然后根据三角形的面积得出m的值,从而得到点A的坐标,然后求出函数解析式;(2)、根据图象得出答案.
试题解析:(1)、在Rt△OAC中,设OC=m,∵tan∠AOC=![]() =2,∴AC=2×OC=2m,
=2,∴AC=2×OC=2m,
∵S△OAC=![]() ×OC×AC=
×OC×AC=![]() ×m×2m=1, ∴m2=1,∴m=±1(负值舍去), ∴A点的坐标为(1,2),
×m×2m=1, ∴m2=1,∴m=±1(负值舍去), ∴A点的坐标为(1,2),
把A点的坐标代入y1=![]() 中,得k1=2, ∴反比例函数的表达式为y1=
中,得k1=2, ∴反比例函数的表达式为y1=![]() ,
,
把A点的坐标代入y2=k2x+1中,得k2+1=2,∴k2=1, ∴一次函数的表达式y2=x+1;
(2)、B点的坐标为(-2,-1), 当0<x<1和x<-2时,y1>y2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了提倡“绿色”出行,顺义区启动了公租自行车项目,为了解我区居民公租自行车的使用情况,某校的社团把使用情况分为A(经常租用)、B(偶尔租用)、C(不使用)三种情况.先后在2015年1月底和3月底做了两次调查,并根据调查结果绘制成了如下两幅不完整的统计图:

根据以上信息解答下列问题:
(1)在扇形统计图中,A(经常租用)所占的百分比是 ;
(2)求两次共抽样调查了多少人;并补全折线统计图;
(3)根据调查的结果,请你谈谈从2015年1月底到2015年3月底,我区居民使用公租自行车的变化情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计图表:
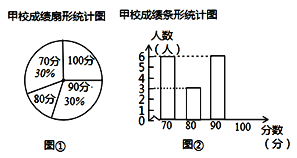
乙校成绩统计表
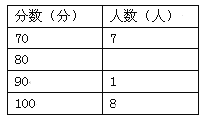
(1)在图①中,“80分”所在扇形的圆心角度数为 ;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;![]()
(4)经计算知S甲2=135,S乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 若a>b,b<c,则a>c B. 若a>b,则ac>bc
C. 若a>b,则ac2>bc2 D. 若ac2>bc2,则a>b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
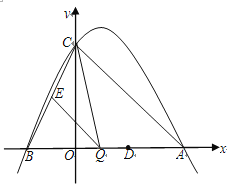
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ,当△CQE的面积为3时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com