
【题目】如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.

(1)求证:AD⊥CD;(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
【答案】(1)、证明过程见解析;(2)、2.5
【解析】
试题分析:(1)、连接OC,根据OA=OC得出∠OAC=∠OCA,根据AC平分∠DAB得到∠OAC=∠DAC,从而说明∠OCA=∠DAC,得到AD∥OC,从而说明切线;(2)、连接CB,根据AB为直径得到∠ACB=90°,根据已知条件得到∠ADC=90°,结合∠DAC=∠CAB得到△DAC∽△CAB,从而得出AB的长度.
试题解析:(1)、连接OC
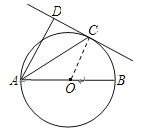
∵OA=OC ∴∠OAC=∠OCA
∵AC平分∠DAB ∴∠OAC=∠DAC ∴∠OCA=∠DAC ∴AD∥OC
∵直线CD与⊙O相切 ∴OC⊥CD ∴AD⊥CD
(2)、连接CB
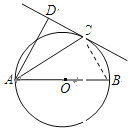
∵AB是⊙O直径 ∴∠ACB=90°
由(1)知AD⊥CD ∴∠ADC=90°∴∠ADC=∠ACB ∵∠DAC=∠CAB ∴△DAC∽△CAB
∴![]() 即
即![]() ∴AB=2.5
∴AB=2.5


科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() (k1﹥0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.
(k1﹥0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.

(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水“五水共治”的重大决策,某中学为了提高学生参与“五水共治”的积极性举行了“五水共治”知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已汇制成如图所示的两幅不完整的统计图,根据图中所经信息解答下列问题:
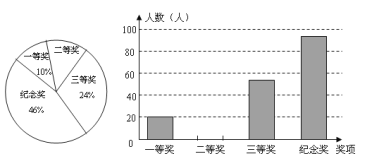
(1)这次知识竞赛共有多少名学生?
(2)浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水“五水共治”的重大决策, “二等奖”对应的扇形圆心角度数,并将条形统计图补充完整;
(3)小华参加了此次的知识竞赛,请你帮他求出获得“一等奖或二等奖”的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】地球上的海洋面积约为361000000平方千米,用科学计数法表示为( )
A. 3.61×109平方千米 B. 3.61×108 平方千米
C. 3.61×107 平方千米 D. 36.1×106 平方千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面正确的命题中,其逆命题不成立的是 ( )
A.同旁内角互补,两直线平行
B.全等三角形的对应边相等
C.角平分线上的点到这个角的两边的距离相等
D.对顶角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若将抛物线y=2x2-4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用反证法证明命题:“在三角形中,至多有一个内角是直角”,正确的假设是( )
A.在三角形中,至少有一个内角是直角B.在三角形中,至少有两个内角是直角
C.在三角形中,没有一个内角是直角D.在三角形中,至多有两个内角是直角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com