
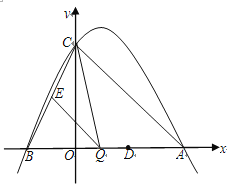
【题目】如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ,当△CQE的面积为3时,求点Q的坐标;
(3)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)、y=-![]() x2+x+4;(2)、Q(1,0);(3)、P(1+
x2+x+4;(2)、Q(1,0);(3)、P(1+![]() ,2 )或P(1-
,2 )或P(1-![]() ,2 )或P(1+
,2 )或P(1+![]() ,3)或P(1-
,3)或P(1-![]() ,3).
,3).
【解析】试题分析:(1)、首先将A、C两点代入求出函数解析式;(2)、首先根据函数解析式得出点B的坐标,求出AB和BQ的长度,根据QE∥AC得出△BQE和△BAC相似得出EG的长度,然后根据三角形的面积得出点m的值,即得到点Q的坐标;(3)、根据DO=DF,FO=FD,OD=OF三种情况分别进行计算,得出点P的坐标.
试题解析:(1)由题意,得![]() ,解得
,解得![]() , ∴所求抛物线的解析式为y=-x2+x+4
, ∴所求抛物线的解析式为y=-x2+x+4
(2)如图,设点Q的坐标为(m,0),过点E作EG⊥x轴于点G,由-x2+x+4=0,

得x1=-2,x2=4,∴点B的坐标为(-2,0) ,∴AB=6,BQ=" m" +2
∵QE∥AC, ∴△BQE∽△BAC ,∴= 即=,∴EG=
∴ S△CQE=S△CBQ-S△EBQ=BQ·CO-BQ·EG =(m+2)(4-) =-m2+m+=3,
∴ m2-2m-8=-9, ∴m=1 ∴Q(1,0)
(3)存在
在△ODF中,
①若DO=DF,∵A(4,0),D(2,0),∴AD=OD=DF=2,又在Rt△AOC中,OA=OC=4,∴∠OAC= 45°
∴∠DFA=∠OAC= 45°∴∠ADF=90°此时,点F的坐标为(2,2)
由![]() ,得x1=1+,x2=1-
,得x1=1+,x2=1-
此时,点P的坐标为:P(1+,2 )或P(1-,2 )
②如图,

若FO=FD,过点F作FM⊥ 轴于点M,由等腰三角形的性质得:OM=OD=1,∴AM=3
∴在等腰直角三角形△AMF中,MF=AM=3 ∴F(1,3)
由-x2+x+4=3,得x1=1+,x2=1-
此时,点P的坐标为:P(1+,3)或P(1-,3)
③若OD=OF,∵OA=OC=4,且∠AOC=90°,∴AC= 4
∴点O到AC的距离为2,而OF=OD=2<2
此时,不存在这样的直线l,使得△ODF是等腰三角形.
综上所述,存在这样的直线l,使得△ODF是等腰三角形.所求点P的坐标为:
P(span>1+,2 )或P(1-,2 )或P(1+,3)或P(1-,3)


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】下列关于有序数对的说法正确的是( )
A.(3,2)与(2,3)表示的位置相同
B.(a,b)与(b, a)表示的位置不同
C.(3,+2)与(+2,3)是表示不同位置的两个有序数对
D.(4, 4)与(4,4)表示两个不同的位置
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y1=![]() (k1﹥0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.
(k1﹥0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.

(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年共有7万名考生参加中考,为了了解这7万名考生的数学成绩,从中抽取了1000名考生的数学成绩进行统计分析.以下说法正确的有( )个.
①这种调查采用了抽样调查的方式
②7万名考生是总体
③1000名考生是总体的一个样本
④每名考生的数学成绩是个体.
A. 2 B. 3 C. 4 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水“五水共治”的重大决策,某中学为了提高学生参与“五水共治”的积极性举行了“五水共治”知识竞赛,所有参赛学生分别设有一、二、三等奖和纪念奖,获奖情况已汇制成如图所示的两幅不完整的统计图,根据图中所经信息解答下列问题:
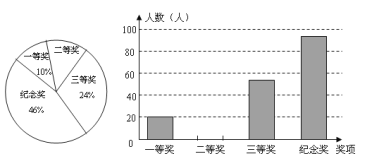
(1)这次知识竞赛共有多少名学生?
(2)浙江省委十三届四次全会提出,要以治污水、防洪水、排涝水、保供水、抓节水“五水共治”的重大决策, “二等奖”对应的扇形圆心角度数,并将条形统计图补充完整;
(3)小华参加了此次的知识竞赛,请你帮他求出获得“一等奖或二等奖”的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若将抛物线y=2x2-4x+3先向右平移3个单位长度,再向上平移2个单位长度,则经过这两次平移后所得抛物线的顶点坐标是__________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com