
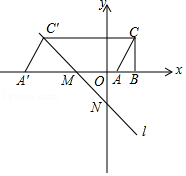
【题目】如图,直线l与x轴,y轴分别交于M,N两点,且OM=ON=3.
(1)求这条直线的函数表达式;
(2)Rt△ABC与直线l在同一个平面直角坐标系内,其中∠ABC=90°,AC=2 ![]() ,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.
,A(1,0),B(3,0),将△ABC沿着x轴向左平移,当点C落在直线l上时,求线段AC扫过的面积.
【答案】
(1)
解:设该直线的函数表达式为y=kx+b(k≠0),
∵OM=ON=3,且M、N分别在x轴负半轴、y轴负半轴上,
∴M(﹣3,0),N(0,﹣3).
将M(﹣3,0)、N(0,﹣3)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴这条直线的函数表达式为y=﹣x﹣3.
(2)
解:∵A(1,0),B(3,0),
∴AB=2.
∵∠ABC=90°,AC=2 ![]() ,
,
∴BC=4,
∴C(3,4).
设平移后点A、C的对应点分别为A′、C′,
当y=﹣x﹣3=4时,x=﹣7,
∴C′(﹣7,4),
∴CC′=10.
∵线段AC扫过的四边形ACC′A′为平行四边形,
∴S=CC′BC=10×4=40.
答:线段AC扫过的面积为40.
【解析】(1)根据OM=ON=3结合图形可得出点M、N的坐标,由点M、N的坐标利用待定系数法即可求出直线MN的函数表达式;(2)通过解直角三角形可得出点C的坐标,设平移后点A、C的对应点分别为A′、C′,利用一次函数图象上点的坐标特征可找出点C′的坐标,根据平移的性质结合平行四边形的面积公式即可求出线段AC扫过的面积.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.
(1)求每个小矩形的长与宽;
(2)在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1 , E2…表示)
(3)求sin∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( ) 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=45°,AD⊥BC于点D,点E在AD上,且DE=DC. 
(1)求证:△BDE≌△ADC;
(2)若BC=8.4,tanC= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由12个形状、大小完全相同的小矩形组成一个大的矩形网格,小矩形的顶点称为这个矩形网格的格点,已知这个大矩形网格的宽为4,△ABC的顶点都在格点.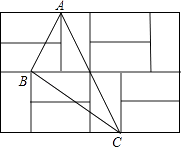
(1)求每个小矩形的长与宽;
(2)在矩形网格中找出所有的格点E,使△ABE为直角三角形;(描出相应的点,并分别用E1 , E2…表示)
(3)求sin∠ACB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作为武汉市政府民生实事之一的公共自行车建设工作已基本完成,“摩拜单车”等租车服务进入市民的生活.某部门对今年5月份一周中的连续7天进行了公共自行车日租车量的统计,并绘制了如下条形图:
(1) 求这7天日租车量的众数与中位数;
(2) 求这7天日租车量的平均数,并用这个平均数估计5月份(31天)共租车多少万车次?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. 
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各组数中,以它们为边长的线段不能构成直角三角形的是 ( )
A. 3, 4, 5 B. ![]() C. 30, 40, 50 D. 0.3, 0.4, 0.5
C. 30, 40, 50 D. 0.3, 0.4, 0.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com