
【题目】如图,已知a∥b,长方形ABCD的点A在直线a上,B,C,D三点在平面上移动变化(长方形形状大小始终保持不变),请根据如下条件解答: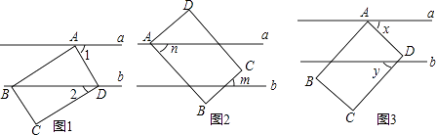
(1)图1,若点B、D在直线b上,点C在直线b的下方,∠2=30°,则∠1=;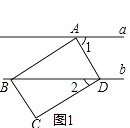
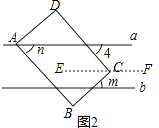
(2)图2,若点D在直线a的上方,点C在平行直线a,b内,点B在直线b的下方,m,n表示角的度数,请说明m与n的数量关系;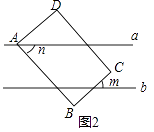
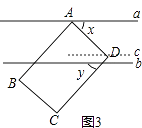
(3)图3,若点D在平行直线a,b内,点B,C在直线b的下方,x,y表示角的度数(x>y),且满足关系式x2﹣2xy+y2=100,求x的度数.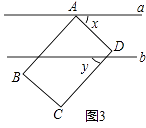
【答案】
(1)60°
(2)
解:如图2,过C作EF∥a,
∵AB∥CD,
∴n=∠4,
∵a∥b,
∴EF∥a∥b,
∴∠4+m=∠BCD=90°,
∴m+n=90°
(3)
解:如图3,过D作c∥b,
∵a∥b,
∴a∥b∥c,
∵x2﹣2xy+y2=100,
∴(x﹣y)2=100,
∵x>y,
∴x﹣y=﹣10(舍去),
∴x﹣y=10,①
∵a∥b,
∴a∥b∥c,
∵∠ADC=90°,
∴x+y=90,②
① +②得:x=50°.
【解析】解:(1)∵四边形ABCD是长方形,
∴∠ADC=90°,
∵∠2=30°,
∴∠ADB=60°,
∵a∥b,
∴∠1=∠ADB=60°,
故答案为:60°;
(1)首先根据角的和差关系计算出∠ADB的度数,再根据平行线的性质可得∠1的度数;(2)过C作EF∥a,根据a∥b可得EF∥a∥b,根据平行线的性质可得∠4+m=∠BCD,n=∠4,利用等量代换可得答案;(3)过D作c∥b,根据条件可得x﹣y=10,再根据平行线的性质可得x+y=90,两个方程组合可得答案.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】2008年8月8日北京奥运会开幕式在国家体育场“鸟巢”举行.“鸟巢”建筑面积为2580000000cm2 , 数字2580000000用科学记数法表示为( )
A.258×107
B.25.8×108
C.2.58×109
D.2.58×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为10的菱形ABCD中,对角线BD=16,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.
(1)对角线AC的长是 ,菱形ABCD的面积是 ;
(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;
(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变,请说明理由,若变化,请探究OE、OF之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( ) (1.)∠C′EF=32°(2)∠AEC=116°(3.)∠BGE=64° (4.)∠BFD=116°.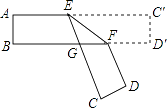
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB是⊙O的切线,AF是⊙O的直径,CN⊥AF于点N,BG⊥AF于点G,连接AB交CN于点M.
(1)写出与点B有关的三条不同类型的结论.(2)、若AG=3FG,求tanA的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com