
【题目】综合与实践
背景阅读:旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动,其中“旋”是过程,“转”是结果.旋转作为图形变换的一种,具备图形旋转前后对应点到旋转中心的距离相等:对应点与旋转中心所连线段的夹角等于旋转角:旋转前、后的图形是全等图形等性质.所以充分运用这些性质是在解决有关旋转问题的关健.
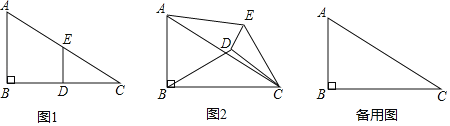
实践操作:如图1,在Rt△ABC中,∠B=90°,BC=2AB=12,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
问题解决:(1)①当α=0°时,![]() = ;②当α=180°时,
= ;②当α=180°时,![]() = .
= .
(2)试判断:当0°≤a<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
问题再探:(3)当△EDC旋转至A,D,E三点共线时,求得线段BD的长为 .
【答案】(1)①![]() ,②
,②![]() ;(2)无变化,证明见解析;(3)6
;(2)无变化,证明见解析;(3)6![]() 或
或![]() .
.
【解析】
问题解决:(1)①根据三角形中位线定理可得:BD=CD![]() BC=6,AE=CE
BC=6,AE=CE![]() AC=3
AC=3![]() ,即可求出
,即可求出![]() 的值;
的值;
②先求出BD,AE的长,即可求出![]() 的值;
的值;
(2)证明△ECA∽△DCB,可得![]() ;
;
问题再探:(3)分两种情况讨论,由矩形的判定和性质以及相似三角形的性质可求BD的长.
问题解决:
(1)①当α=0°时.
∵BC=2AB=12,
∴AB=6,
∴AC![]() 6
6![]() ,
,
∵点D、E分别是边BC、AC的中点,
∴BD=CD![]() BC=6,AE=CE
BC=6,AE=CE![]() AC=3
AC=3![]() ,DE
,DE![]() AB,
AB,
∴![]() .
.
故答案为:![]() ;
;
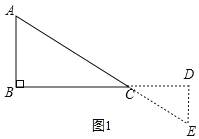
②如图1.
 ,
,
当α=180°时.
∵将△EDC绕点C按顺时针方向旋转,
∴CD=6,CE=3![]() ,
,
∴AE=AC+CE=9![]() ,BD=BC+CD=18,
,BD=BC+CD=18,
∴![]() .
.
故答案为:![]() .
.
(2)如图2,
 ,
,
当0°≤α<360°时,![]() 的大小没有变化.证明如下:
的大小没有变化.证明如下:
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵![]() ,
,
∴△ECA∽△DCB,
∴![]() .
.
问题再探:
(3)分两种情况讨论:
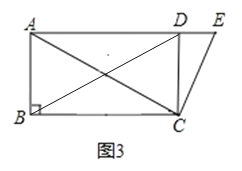
①如图3.
 .
.
∵AC=6![]() ,CD=6,CD⊥AD,
,CD=6,CD⊥AD,
∴AD![]() 12.
12.
∵AD=BC,AB=DC,
∴四边形ABCD是平行四边形.
∵∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=6![]()
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P.
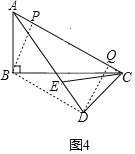
∵AC=6![]() ,CD=6,CD⊥AD,
,CD=6,CD⊥AD,
∴AD![]() 12.
12.
在Rt△CDE中,DE=![]() =3,
=3,
∴AE=AD﹣DE=12﹣3=9,
由(2)可得:![]() ,
,
∴BD .
.
综上所述:BD=6![]() 或
或![]() .
.
故答案为:6![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
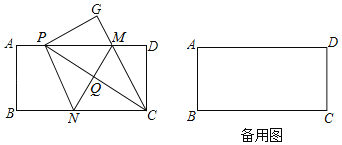
【题目】如图,现有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN丁点Q,连接CM.
(1)求证:PM=PN;
(2)当P,A重合时,求MN的值;
(3)若△PQM的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,学生会随机抽取了20名七、八年级学生(每个年级各10人)进行问卷调查,并把他们的得分绘制成了如下表格,计分采用10分制(得分均取整数)成绩达到6分或6分以上为及格,达到9分及以上为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
七年级 | 5 | 8 | 8 |
| 8 | 10 | 10 | 8 | 5 | 5 |
八年级 | 10 | 6 | 6 | 9 |
| 4 | 5 | 7 | 10 | 8 |
表2
年级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
七年级 | 7.6 | 8 | 8 | 3.82 | 70% |
|
八年级 | 7.5 |
| 10 | 4.94 | 80% | 40% |
(1)在表1中,![]() _____,
_____,![]() _____;在表2中,
_____;在表2中,![]() _____,
_____,![]() ______;
______;
(2)根据表2成绩数据分析,你认为哪个年级的学生对垃圾分类了解更加深入,请说明你的理由;
(3)小明根据表2数据作出如下判断:
①七年级学生成绩的平均数高于八年级,故七年级学生一定比八年级学生优秀;
②被调查对象中,七年级学生的成绩更加稳定;
③学校七年级和八年级共有400人,估计有280人成绩达到优秀;
④七年级不及格人数比八年级多;
对小明的四个结论,随机任选两个,求都是错误的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
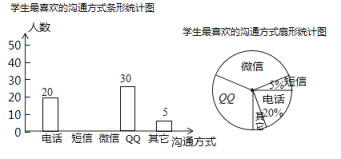
(1)这次统计共抽查了多少名学生?在扇形统计图中,表示" ![]() "的扇形圆心角的度数是多少;
"的扇形圆心角的度数是多少;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?
(4)某天甲、乙两名同学都想从“微信"、"![]() "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
"、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
(1)甲船从C处出发追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
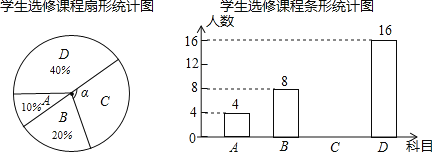
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整;
(3)学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=45°,∠ACB=30°,将△ABC绕点A顺时针旋转得到△AB1C1,当点C1、B1、C三点共线时,旋转角为α,连接BB1,交AC于点D.下列结论:①△AC1C为等腰三角形;②△AB1D∽△BCD;③α=75°;④CA=CB1,其中正确的是( )
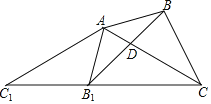
A.①③④B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
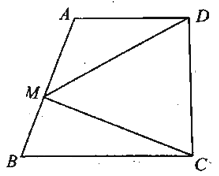
【题目】如图,在直角梯形 ABCD 中,AD / /BC ,AD CD ,M 为腰 AB 上一动点,联结 MC 、MD , AD 10, BC 15 , cot B ![]() ,求:
,求:
(1)线段CD 的长.
(2)设线段 BM 的长为 x ,△CDM的面积为 y ,求 y 关于 x 的函数解析式,并写出它的定义域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com