练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

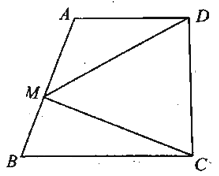
    【题目】如图，在直角梯形 ABCD 中，AD / /BC ，AD CD ，M 为腰 AB 上一动点，联结 MC 、MD ， AD 10， BC 15 ， cot B ，求：

    （1）线段CD 的长.

    （2）设线段 BM 的长为 x ，△CDM的面积为 y ，求 y 关于 x 的函数解析式，并写出它的定义域.

    【答案】（1）CD=12；（2）y=-（ 0 ＜x＜13 ）.

    【解析】

    (1)做AM垂直BC于M，根据条件即可解答.

    (2) 做MN垂直BC于N，,根据三角函数求出NC即可解答.

    解：（1）做AE垂直BC于M，则BE=15-10=5.

    又因为cotB=,BE=5,

    可得AE=12，即CD=12.

    (2)做MN垂直BC于N，则BN=x,CN=15-x,

    即y=×12×（15-x）=-x+90,(定义域为0≤x≤13).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    背景阅读：旋转就是将图形上的每一点在平面内绕着旋转中心旋转固定角度的位置移动，其中“旋”是过程，“转”是结果．旋转作为图形变换的一种，具备图形旋转前后对应点到旋转中心的距离相等：对应点与旋转中心所连线段的夹角等于旋转角：旋转前、后的图形是全等图形等性质．所以充分运用这些性质是在解决有关旋转问题的关健．

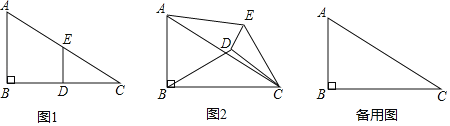
    实践操作：如图1，在Rt△ABC中，∠B＝90°，BC＝2AB＝12，点D，E分别是边BC，AC的中点，连接DE，将△EDC绕点C按顺时针方向旋转，记旋转角为α．

    问题解决：（1）①当α＝0°时，＝　 　；②当α＝180°时，＝　 　．

    （2）试判断：当0°≤a＜360°时，的大小有无变化？请仅就图2的情形给出证明．

    问题再探：（3）当△EDC旋转至A，D，E三点共线时，求得线段BD的长为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0；②4a+2b+c＞0；③＜a＜；④b＞c．其中含所有正确结论的选项是（ ）

    A.①②③B.①③④C.②③④D.①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，中，，，于点，点是线段的一个动点，则的最小值是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC 与△DEF 中，下列四个命题是真命题的个数共有（ ）

    ①如果A D, ，那么△ABC 与△DEF相似；

    ②如果A D,，那么△ABC 与△DEF相似；

    ③如果A D 90°，,那么△ABC 与△DEF相似；

    ④如果A D 90°, ，那么△ABC 与△DEF相似．

    A.1 个B.2 个C.3 个D.4 个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y1=ax+b的图象与反比例函数y2=的图象相交于A、B两点，坐标分别为（—2，4）、（4，—2）．

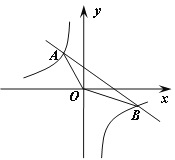
    （1）求两个函数的解析式；

    （2）求△AOB的面积；

    （3）直线AB上是否存在一点P（A除外），使△ABO与以B﹑P、O为顶点的三角形相似？若存在，直接写出顶点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近期猪肉价格不断走高，引起了民众与政府的高度关注．当市场猪肉的平均价格每千克达到一定的单价时，政府将投入储备猪肉以平抑猪肉价格．

    （1）从去年年底至今年3月20日，猪肉价格不断走高，3月20日比去年年底价格上涨了60%．某市民在今年3月20日购买2.5千克猪肉至少要花200元钱，那么去年年底猪肉的最低价格为每千克多少元？

    （2）3月20日，猪肉价格为每千克60元，3月21日，某市决定投入储备猪肉并规定其销售价在每千克60元的基础上下调a%出售．某超市按规定价出售一批储备猪肉，该超市在非储备猪肉的价格仍为每千克60元的情况下，该天的两种猪肉总销量比3月20日增加了a%，且储备猪肉的销量占总销量的，两种猪肉销售的总金额比3月20日提高了，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

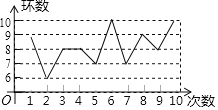
    【题目】2019年第七届世界军人运动会（7thCISMMilitaryWorldGames）于2019年10月18日至27日在中国武汉举行，这是中国第一次承办综合性国际军事赛事，也是继北京奥运会后，中国举办的规模最大的国际体育盛会．某射击运动员在一次训练中射击了10次，成绩如图所示．下列结论中不正确的有（　　）个

    ①众数是8；②中位数是8；③平均数是8；④方差是1.6．

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

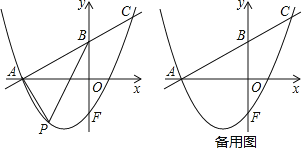
    【题目】如图，已知在平面直角坐标系xOy中，直线y＝x+与x轴交于点A，与y轴交于点B，点F是点B关于x轴的对称点，抛物线y＝x2+bx+c经过点A和点F，与直线AB交于点C．

    （1）求b和c的值；

    （2）点P是直线AC下方的抛物线上的一动点，连结PA，PB．求△PAB的最大面积及点P到直线AC的最大距离；

    （3）点Q是抛物线上一点，点D在坐标轴上，在（2）的条件下，是否存在以A，P，D，Q为顶点且AP为边的平行四边形，若存在，直接写出点Q的坐标；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案