
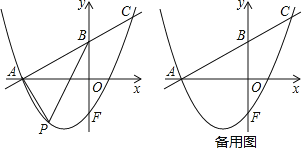
【题目】如图,已知在平面直角坐标系xOy中,直线y=![]() x+
x+![]() 与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=
与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=![]() x2+bx+c经过点A和点F,与直线AB交于点C.
x2+bx+c经过点A和点F,与直线AB交于点C.
(1)求b和c的值;
(2)点P是直线AC下方的抛物线上的一动点,连结PA,PB.求△PAB的最大面积及点P到直线AC的最大距离;
(3)点Q是抛物线上一点,点D在坐标轴上,在(2)的条件下,是否存在以A,P,D,Q为顶点且AP为边的平行四边形,若存在,直接写出点Q的坐标;若不存在,说明理由.
【答案】(1)b=![]() ,c=﹣
,c=﹣![]() ;(2)
;(2)![]() ,
,![]() ;(3)点Q的坐标为:(﹣1﹣
;(3)点Q的坐标为:(﹣1﹣![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(﹣1+
)或(﹣1+![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
(1)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,则点
,则点![]() 、
、![]() 的坐标分别为:
的坐标分别为:![]() 、
、![]() ,则点
,则点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 和点
和点![]() ,则
,则![]() ,将点
,将点![]() 的坐标代入抛物线表达式并解得:
的坐标代入抛物线表达式并解得:![]() ;
;
(2)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设出点P,H的坐标,将△PAB的面积表示成△APH和△BPH的面积之和,可得函数表达式,可求△PAB的面积最大值,此时设点P到AB的距离为d,当△PAB的面积最大值时d最大,利用面积公式求出d.
,设出点P,H的坐标,将△PAB的面积表示成△APH和△BPH的面积之和,可得函数表达式,可求△PAB的面积最大值,此时设点P到AB的距离为d,当△PAB的面积最大值时d最大,利用面积公式求出d.
(3)若存在以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点且
为顶点且![]() 为边的平行四边形时,平移AP,得出所有可能的情形,利用平行四边形的对称性得到坐标的关系,即可求解.
为边的平行四边形时,平移AP,得出所有可能的情形,利用平行四边形的对称性得到坐标的关系,即可求解.
解:(1)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
令x=0,则y=![]() ,令y=0,则x=-3,
,令y=0,则x=-3,
则点![]() 、
、![]() 的坐标分别为:
的坐标分别为:![]() 、
、![]() ,
,
∵点F是点B关于x轴的对称点,
∴点![]() ,
,
∵抛物线![]() 经过点
经过点![]() 和点
和点![]() ,则
,则![]() ,
,
将点![]()
![]() 代入抛物线表达式得:
代入抛物线表达式得:![]() ,
,
解得:![]() ,
,
故抛物线的表达式为:![]() ,
,
![]() ,
,![]() ;
;
(2)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,
,
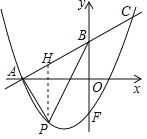
设点![]() ,则点
,则点![]() ,
,
则![]() 的面积:
的面积:
![]()
![]()
当![]() 时,
时,
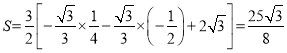 ,
,
且![]() ,
,
∴![]() 的最大值为
的最大值为![]() ,此时点
,此时点![]() ,
,![]() ,
,
设:![]() 到直线
到直线![]() 的最大距离为
的最大距离为![]() ,
,![]()
![]() ,解得:
,解得:![]() ;
;
(3)存在,理由:
点![]() ,点
,点![]() ,
,![]() ,设点
,设点![]() ,
,![]() ,
,
①当点![]() 在
在![]() 轴上时,
轴上时,
若存在以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点且
为顶点且![]() 为边的平行四边形时,如图,
为边的平行四边形时,如图,
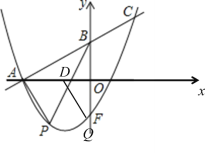
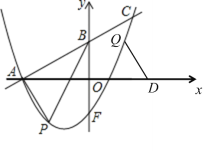
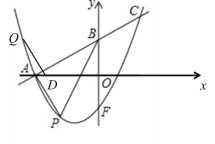
三种情形都可以构成平行四边形,
由于平行四边形的对称性可得图中点Q到x轴的距离和点P到x轴的距离相等,
∴![]() ,
,
即![]() ,
,
解得:![]() (舍去)或
(舍去)或![]() 或
或![]() ;
;
②当点![]() 在
在![]() 轴上时,如图:
轴上时,如图:
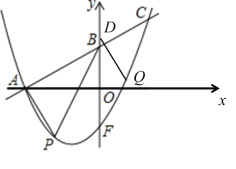
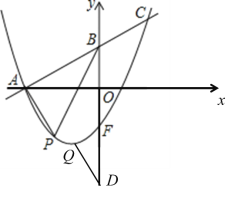
当点Q在y轴右侧时,由平行四边形的性质可得:
![]() =3,
=3,
∴![]()
∴m=![]() ,代入二次函数表达式得:y=
,代入二次函数表达式得:y=![]()
当点Q在y轴左侧时,由平行四边形的性质可得:
![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,代入二次函数表达式得:y=
,代入二次函数表达式得:y=![]()
故点![]() ,
,![]() 或
或![]() ,
,![]() ;
;
故点![]() 的坐标为:
的坐标为:![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() 或
或![]() ,
,![]() .
.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
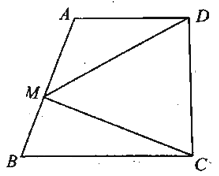
【题目】如图,在直角梯形 ABCD 中,AD / /BC ,AD CD ,M 为腰 AB 上一动点,联结 MC 、MD , AD 10, BC 15 , cot B ![]() ,求:
,求:
(1)线段CD 的长.
(2)设线段 BM 的长为 x ,△CDM的面积为 y ,求 y 关于 x 的函数解析式,并写出它的定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“学雷锋、树新风、做文明中学生”的号召,某校开展了志愿者服务活动,活动项目有“防疫宜宣传”、“文明交通岗”、“关爱老人”、“义务植树”、“社区服务”五项,活动期间,随机抽取了部分学生对志思者服务情况进行调查,结果发现,被调查的每名学生都参与了活动,最少的参与了1项,最多的参与了5项,根据调查结果绘制了如下不完整的条形统计图和扇形统计图.
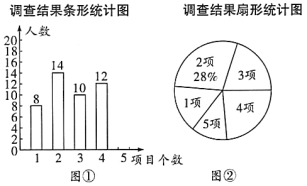
根据以上统计图解答下列问题:
(1)本次随机抽取的学生共有______名;
(2)补全条形统计图;
(3)若该校有3000名学生,请估计参与了4项活动的学生人数;
(4)在所调查的学生中随机选取一人谈活动心得,求选中参与了5项活动的学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为贯彻落实“绿水青山就是金山银山“的发展理念,投资组建了日废水处理量为m吨的废水处理车间,对该厂工业废水进行无害化处理. 但随着工厂生产规模的扩大,该车间经常无法完成当天工业废水的处理任务,需要将超出日废水处理量的废水交给第三方企业处理. 已知该车间处理废水,每天需固定成本30元,并且每处理一吨废水还需其他费用8元;将废水交给第三方企业处理,每吨需支付12元.根据记录,5月21日,该厂产生工业废水35吨,共花费废水处理费370元.
(1)求该车间的日废水处理量m;
(2)为实现可持续发展,走绿色发展之路,工厂合理控制了生产规模,使得每天废水处理的平均费用不超过10元/吨,试计算该厂一天产生的工业废水量的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
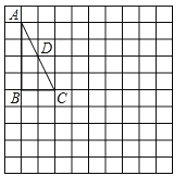
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 的中点,请按下列要求作图,并解决问题:
的中点,请按下列要求作图,并解决问题:
(1)作点![]() 关于
关于![]() 的对称点
的对称点![]() ;
;
(2)在(1)的条件下,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,
,
①面出旋转后的![]() (其中
(其中![]() 、
、![]() 、
、![]() 三点旋转后的对应点分别是点
三点旋转后的对应点分别是点![]() 、
、![]() 、
、![]() );
);
②若![]() ,则
,则![]() ________.(用含
________.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为( )

A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com