
【题目】如图,在圆O中,直径AB平分弦CD于点E,且CD=4![]() ,连接AC,OD,若∠A与∠DOB互余,则EB的长是( )
,连接AC,OD,若∠A与∠DOB互余,则EB的长是( )

A.2![]() B.4C.
B.4C.![]() D.2
D.2
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】近期猪肉价格不断走高,引起了民众与政府的高度关注.当市场猪肉的平均价格每千克达到一定的单价时,政府将投入储备猪肉以平抑猪肉价格.
(1)从去年年底至今年3月20日,猪肉价格不断走高,3月20日比去年年底价格上涨了60%.某市民在今年3月20日购买2.5千克猪肉至少要花200元钱,那么去年年底猪肉的最低价格为每千克多少元?
(2)3月20日,猪肉价格为每千克60元,3月21日,某市决定投入储备猪肉并规定其销售价在每千克60元的基础上下调a%出售.某超市按规定价出售一批储备猪肉,该超市在非储备猪肉的价格仍为每千克60元的情况下,该天的两种猪肉总销量比3月20日增加了a%,且储备猪肉的销量占总销量的![]() ,两种猪肉销售的总金额比3月20日提高了
,两种猪肉销售的总金额比3月20日提高了![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
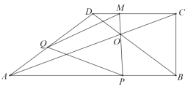
【题目】已知:如图,四边形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 开始沿
开始沿![]() 边匀速运动,运动速度为
边匀速运动,运动速度为![]() ,动点
,动点![]() 从点
从点![]() 开始沿
开始沿![]() 边匀速运动,运动速度为
边匀速运动,运动速度为![]() .点
.点![]() 和点
和点![]() 同时出发,
同时出发,![]() 为四边形
为四边形![]() 的对角线的交点,连接
的对角线的交点,连接![]() 并延长交
并延长交![]() 于
于![]() ,连接
,连接![]() .设运动的时间为
.设运动的时间为![]() ,
,![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() 的面积等于五边形
的面积等于五边形![]() 面积的
面积的![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 在
在![]() 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
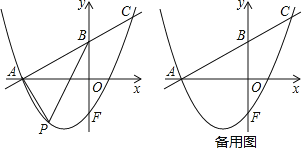
【题目】如图,已知在平面直角坐标系xOy中,直线y=![]() x+
x+![]() 与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=
与x轴交于点A,与y轴交于点B,点F是点B关于x轴的对称点,抛物线y=![]() x2+bx+c经过点A和点F,与直线AB交于点C.
x2+bx+c经过点A和点F,与直线AB交于点C.
(1)求b和c的值;
(2)点P是直线AC下方的抛物线上的一动点,连结PA,PB.求△PAB的最大面积及点P到直线AC的最大距离;
(3)点Q是抛物线上一点,点D在坐标轴上,在(2)的条件下,是否存在以A,P,D,Q为顶点且AP为边的平行四边形,若存在,直接写出点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
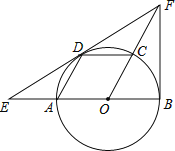
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,且四边形
上,且四边形![]() 是平行四边形,过点
是平行四边形,过点![]() 作
作![]() 的切线,分别交
的切线,分别交![]() 的延长线与
的延长线与![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 。
。
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径为1,求
的半径为1,求![]() 的长。
的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.
(1)当∠OAD=30°时,求点C的坐标;
(2)设AD的中点为M,连接OM、MC,当四边形OMCD的面积为![]() 时,求OA的长;
时,求OA的长;
(3)当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果店主分两批购进同一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果每箱的单价是多少元?
(2)该水果店主计划两批水果的售价均定为每千克4元,每箱10千克,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了2%的损耗,但这两批水果销售完后仍赚了不低于2346元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从青岛到济南有南线和北线两条高速公路:南线全长400千米,北线全长320千米.甲、乙两辆客车分别由南线和北线从青岛驶往济南,已知客车甲在南线高速公路上行驶的平均速度比客车乙在北线高速公路上快20千米/小时,两车恰好同时到达济南,求两辆客车从青岛到济南所用的时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
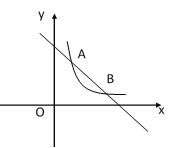
【题目】一次函数y1=kx+b与反比例函数y2=![]() (n>0)交于点A(1,3),B(3,m).
(n>0)交于点A(1,3),B(3,m).
(1)分别求两个函数的解析式;
(2)根据图像直接写出,当x为何值时,y1<y2;
(3)在x轴上找一点P,使得△OAP的面积为6,求出P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com