
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”xOyÖĐŁŹŸŰĐÎABCD”ıßABŁœ4ŁŹBCŁœ6ŁźÈôČ»žÄ±äŸŰĐÎABCD”ÄĐÎŚŽșÍŽóĐĄŁŹ”±ŸŰĐζ„”ăAÔÚxÖá”ÄŐę°ëÖáÉÏŚóÓÒÒƶŻÊ±ŁŹŸŰĐΔÄÁíÒ»žö¶„”ăDÊŒÖŐÔÚyÖá”ÄŐę°ëÖáÉÏËæÖźÉÏÏÂÒƶŻŁź
(1)”±ĄÏOADŁœ30ĄăʱŁŹÇó”ăC”ÄŚű±êŁ»
(2)ÉèAD”ÄÖĐ”ăÎȘMŁŹÁŹœÓOMĄąMCŁŹ”±ËıßĐÎOMCD”ÄĂæ»ęÎȘ![]() ʱŁŹÇóOA”Äł€Ł»
ʱŁŹÇóOA”Äł€Ł»
(3)”±”ăAÒƶŻ”œÄłÒ»Î»ÖĂʱŁŹ”ăC”œ”ăO”ÄŸàÀëÓĐŚîŽóÖ”ŁŹÇëÖ±œÓĐŽłöŚîŽóÖ”ŁŹČąÇóŽËʱcosĄÏOAD”ÄÖ”Łź

ĄŸŽđ°žĄż(1)”ăC”ÄŚű±êÎȘ(2ŁŹ3+2![]() )Ł»(2)OAŁœ3
)Ł»(2)OAŁœ3![]() Ł»(3)OC”ÄŚîŽóÖ”ÎȘ8ŁŹcosĄÏOADŁœ
Ł»(3)OC”ÄŚîŽóÖ”ÎȘ8ŁŹcosĄÏOADŁœ![]() Łź
Łź
ĄŸœâÎöĄż
(1)ŚśCEĄÍyÖᣏÏÈÖ€ĄÏCDEŁœĄÏOADŁœ30Ąă”ĂCEŁœ![]() CDŁœ2ŁŹDEŁœ
CDŁœ2ŁŹDEŁœ![]() ŁŹÔÙÓÉĄÏOADŁœ30ĄăÖȘODŁœ
ŁŹÔÙÓÉĄÏOADŁœ30ĄăÖȘODŁœ![]() ADŁœ3ŁŹŽÓ¶ű”Ăłö”ăCŚű±êŁ»
ADŁœ3ŁŹŽÓ¶ű”Ăłö”ăCŚű±êŁ»
(2)ÏÈÇółöSĄśDCMŁœ6ŁŹœáșÏSËıßĐÎOMCDŁœ![]() ÖȘSĄśODMŁœ
ÖȘSĄśODMŁœ![]() ŁŹSĄśOADŁœ9ŁŹÉèOAŁœxĄąODŁœyŁŹŸĘŽËÖȘx2+y2Łœ36ŁŹ
ŁŹSĄśOADŁœ9ŁŹÉèOAŁœxĄąODŁœyŁŹŸĘŽËÖȘx2+y2Łœ36ŁŹ![]() xyŁœ9ŁŹ”Ăłöx2+y2Łœ2xyŁŹŒŽxŁœyŁŹŽúÈëx2+y2Łœ36Çó”Ăx”ÄÖ”ŁŹŽÓ¶ű”ĂłöŽđ°žŁ»
xyŁœ9ŁŹ”Ăłöx2+y2Łœ2xyŁŹŒŽxŁœyŁŹŽúÈëx2+y2Łœ36Çó”Ăx”ÄÖ”ŁŹŽÓ¶ű”ĂłöŽđ°žŁ»
(3)ÓÉMÎȘAD”ÄÖД㣏ÖȘOMŁœ3ŁŹCMŁœ5ŁŹÓÉOCĄÜOM+CMŁœ8ÖȘ”±OĄąMĄąCÈę”ăÔÚÍŹÒ»Ö±ÏßʱŁŹOCÓĐŚîŽóÖ”8ŁŹÁŹœÓOCŁŹÔòŽËʱOCÓëAD”Äœ»”ăÎȘMŁŹONĄÍADŁŹÖ€ĄśCMDĄŚĄśOMN”Ă![]() ŁŹŸĘŽËÇó”ĂMNŁœ
ŁŹŸĘŽËÇó”ĂMNŁœ![]() ŁŹONŁœ
ŁŹONŁœ![]() ŁŹANŁœAM©MNŁœ
ŁŹANŁœAM©MNŁœ![]() ŁŹÔÙÓÉOAŁœ
ŁŹÔÙÓÉOAŁœ![]() Œ°cosĄÏOADŁœ
Œ°cosĄÏOADŁœ![]() żÉ”Î𰞣ź
żÉ”Î𰞣ź
(1)ÈçÍŒ1ŁŹčę”ăCŚśCEĄÍyÖáÓÚ”ăEŁŹ
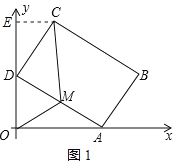
ĄßŸŰĐÎABCDÖĐŁŹCDĄÍADŁŹ
ĄàĄÏCDE+ĄÏADOŁœ90ĄăŁŹ
Ó֥ߥÏOAD+ĄÏADOŁœ90ĄăŁŹ
ĄàĄÏCDEŁœĄÏOADŁœ30ĄăŁŹ
ĄàÔÚRtĄśCEDÖĐŁŹCEŁœ![]() CDŁœ2ŁŹDEŁœ
CDŁœ2ŁŹDEŁœ![]() Łœ2
Łœ2![]() ŁŹ
ŁŹ
ÔÚRtĄśOADÖĐŁŹĄÏOADŁœ30ĄăŁŹ
ĄàODŁœ![]() ADŁœ3ŁŹ
ADŁœ3ŁŹ
Ąà”ăC”ÄŚű±êÎȘ(2ŁŹ3+2![]() )Ł»
)Ł»
(2)ĄßMÎȘAD”ÄÖД㣏
ĄàDMŁœ3ŁŹSĄśDCMŁœ6ŁŹ
ÓÖSËıßĐÎOMCDŁœ![]() ŁŹ
ŁŹ
ĄàSĄśODMŁœ![]() ŁŹ
ŁŹ
ĄàSĄśOADŁœ9ŁŹ
ÉèOAŁœxĄąODŁœyŁŹÔòx2+y2Łœ36ŁŹ![]() xyŁœ9ŁŹ
xyŁœ9ŁŹ
Ąàx2+y2Łœ2xyŁŹŒŽxŁœyŁŹ
œ«xŁœyŽúÈëx2+y2Łœ36”Ăx2Łœ18ŁŹ
œâ”ĂxŁœ3![]() (žșÖ”ÉáÈ„)ŁŹ
(žșÖ”ÉáÈ„)ŁŹ
ĄàOAŁœ3![]() Ł»
Ł»
(3)OC”ÄŚîŽóÖ”ÎȘ8ŁŹ
ÈçÍŒ2ŁŹMÎȘAD”ÄÖД㣏
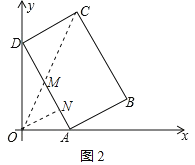
ĄàOMŁœ3ŁŹCMŁœ![]() Łœ5ŁŹ
Łœ5ŁŹ
ĄàOCĄÜOM+CMŁœ8ŁŹ
”±OĄąMĄąCÈę”ăÔÚÍŹÒ»Ö±ÏßʱŁŹOCÓĐŚîŽóÖ”8ŁŹ
ÁŹœÓOCŁŹÔòŽËʱOCÓëAD”Äœ»”ăÎȘMŁŹčę”ăOŚśONĄÍADŁŹŽčŚăÎȘNŁŹ
ĄßĄÏCDMŁœĄÏONMŁœ90ĄăŁŹĄÏCMDŁœĄÏOMNŁŹ
ĄàĄśCMDĄŚĄśOMNŁŹ
Ąà![]() ŁŹŒŽ
ŁŹŒŽ![]() ŁŹ
ŁŹ
œâ”ĂMNŁœ![]() ŁŹONŁœ
ŁŹONŁœ![]() ŁŹ
ŁŹ
ĄàANŁœAM©MNŁœ![]() ŁŹ
ŁŹ
ÔÚRtĄśOANÖĐŁŹOAŁœ![]() ŁŹ
ŁŹ
ĄàcosĄÏOADŁœ![]() Łź
Łź


 ĂûĐŁżÎÌĂÏ”ÁĐŽđ°ž
ĂûĐŁżÎÌĂÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
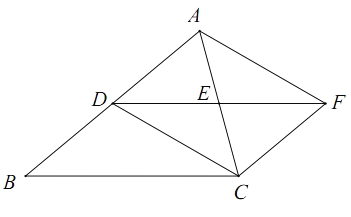
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚĄśABCÖĐŁŹDÎȘABÖД㣏čę”ăDŚśDF//BCœ»ACÓÚ”ăEŁŹÇÒDE=EFŁŹÁŹœÓAFŁŹCFŁŹCDŁź
Łš1Ł©ÇóÖ€ŁșËıßĐÎADCFÎȘÆœĐĐËıßĐÎŁ»
Łš2Ł©ÈôĄÏACD=45ĄăŁŹĄÏEDC=30ĄăŁŹBC=4ŁŹÇóCE”Äł€Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłč€ł§ÎȘčáłčÂäÊ”Ą°ÂÌËźÇàÉœŸÍÊÇœđÉœÒűÉœĄ°”Ä·ąŐčÀíÄͶŚÊŚéœšÁËÈŐ·ÏËźŽŠÀíÁżÎȘm¶Ö”Ä·ÏËźŽŠÀíł”ŒäŁŹ¶ÔžĂł§č€Ò”·ÏËźœűĐĐÎȚșŠ»ŻŽŠÀí. ”«ËæŚĆ耳§ÉúČúčæÄŁ”ÄÀ©ŽóŁŹžĂł”ŒäŸłŁÎȚ·šÍêłÉ”±Ììč€Ò”·ÏËź”ÄŽŠÀíÈÎÎńŁŹĐèÒȘœ«łŹłöÈŐ·ÏËźŽŠÀíÁż”Ä·ÏËźœ»žű”ÚÈę·œÆóÒ”ŽŠÀí. ÒŃÖȘžĂł”ŒäŽŠÀí·ÏËźŁŹĂżÌìĐèč̶šłÉ±Ÿ30ÔȘŁŹČąÇÒĂżŽŠÀíÒ»¶Ö·ÏËź»čĐèÆäËû·ŃÓĂ8ÔȘŁ»œ«·ÏËźœ»žű”ÚÈę·œÆóÒ”ŽŠÀíŁŹĂż¶ÖĐèÖ§ž¶12ÔȘ.žùŸĘŒÇÂŒŁŹ5ÔÂ21ÈŐŁŹžĂł§ČúÉúč€Ò”·ÏËź35¶ÖŁŹčČ»š·Ń·ÏËźŽŠÀí·Ń370ÔȘ.
(1)ÇóžĂł”Œä”ÄÈŐ·ÏËźŽŠÀíÁżmŁ»
(2)ÎȘÊ”ÏֿɳÖĐű·ąŐ裏ŚßÂÌÉ«·ąŐč֟·ŁŹč€ł§șÏÀíżŰÖÆÁËÉúČúčæÄŁŁŹÊč”ĂĂżÌì·ÏËźŽŠÀí”ÄÆœŸù·ŃÓĂČ»łŹčę10ÔȘ/¶ÖŁŹÊÔŒÆËăžĂł§Ò»ÌìČúÉú”Äč€Ò”·ÏËźÁż”Ä·¶Î§.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŒŚĄąÒÒÁœĐŁ·Ö±đÓĐÒ»ÄĐÒ»ĆźčČ4ĂûœÌÊŠ±šĂû”œĆ©ŽćÖĐѧ֧œÌŁź
Łš1Ł©ÈôŽÓŒŚĄąÒÒÁœĐŁ±šĂû”ÄœÌÊŠÖĐ·Ö±đËæ»úŃĄ1ĂûŁŹÔòËùŃĄ”Ä2ĂûœÌÊŠĐÔ±đÏàÍŹ”ÄžĆÂÊÊÇ Łź
Łš2Ł©ÈôŽÓ±šĂû”Ä4ĂûœÌÊŠÖĐËæ»úŃĄ2ĂûŁŹÓĂÁбí»ò»ÊśŚŽÍŒ”Ä·œ·šÇółöŐâ2ĂûœÌÊŠÀŽŚÔÍŹÒ»ËùѧУ”ÄžĆÂÊŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÔČOÖĐŁŹÖ±Ÿ¶ABÆœ·ÖÏÒCDÓÚ”ăEŁŹÇÒCD=4![]() ŁŹÁŹœÓACŁŹOD,ÈôĄÏAÓëĄÏDOB»„ÓàŁŹÔòEB”Äł€ÊÇŁš Ł©
ŁŹÁŹœÓACŁŹOD,ÈôĄÏAÓëĄÏDOB»„ÓàŁŹÔòEB”Äł€ÊÇŁš Ł©

A.2![]() B.4C.
B.4C.![]() D.2
D.2
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
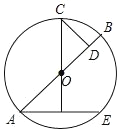
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÖĐĄŃOŁŹAB ÊÇÖ±Ÿ¶ŁŹÏÒ AE ”ÄŽčֱƜ·ÖÏßœ»ĄŃO ÓÚ”ă CŁŹCDĄÍABÓÚ DŁŹBDŁœ1ŁŹAEŁœ4ŁŹÔò AD ”Äł€ÎȘ___Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÈôžÉžöÈ«”È”ÄŐęÎć±ßĐÎĆƳɻ·ŚŽŁŹÍŒÖĐËùÊŸ”ÄÊÇÇ°3žöŐęÎć±ßĐÎŁŹÒȘÍêłÉŐâÒ»ÔČ»·»čĐèŐęÎć±ßĐΔĞöÊęÎȘŁšĄĄĄĄŁ©

A. 10 B. 9 C. 8 D. 7
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
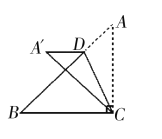
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚ![]() ÖĐ
ÖĐ![]() ŁŹDÊÇб±ßABÉÏ”ÄÒ»žö¶Ż”㣏
ŁŹDÊÇб±ßABÉÏ”ÄÒ»žö¶Ż”㣏![]() ŃŰÖ±ÏßCDŐÛ”țŁŹ”ăAÂäÔÚÍŹÒ»ÆœĂæÄÚ”Ä
ŃŰÖ±ÏßCDŐÛ”țŁŹ”ăAÂäÔÚÍŹÒ»ÆœĂæÄÚ”Ä![]() ŽŠŁŹ”±
ŽŠŁŹ”±![]() DŽčÖ±ÓÚ
DŽčÖ±ÓÚ![]() ”ÄÖ±œÇ±ßʱŁŹAD”Äł€ÎȘ_____Łź
”ÄÖ±œÇ±ßʱŁŹAD”Äł€ÎȘ_____Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŒĂÄțijУÎȘÁËœâŸĆÄêŒ¶Ń§ÉúÒŐÊőČâÊÔÇéżöŁźÒÔŸĆÄꌫŁš1Ł©°àѧÉú”ÄÒŐÊőČâÊÔłÉŒšÎȘŃù±ŸŁŹ°Ž![]() Ąą
Ąą![]() Ąą
Ąą![]() Ąą
Ąą![]() ËÄžö”ÈŒ¶œűĐĐÍłŒÆŁŹČąœ«ÍłŒÆœáčû»æÖÆłÉÈçÏ”ÄÍłŒÆÍŒŁŹÇëÄăœáșÏÍŒÖĐËùžűĐĆÏąœâŽđÏÂÁĐÎÊÌâŁș
ËÄžö”ÈŒ¶œűĐĐÍłŒÆŁŹČąœ«ÍłŒÆœáčû»æÖÆłÉÈçÏ”ÄÍłŒÆÍŒŁŹÇëÄăœáșÏÍŒÖĐËùžűĐĆÏąœâŽđÏÂÁĐÎÊÌâŁș

ŁšË”ĂśŁș![]() Œ¶Łș90·Ö~100·ÖŁ»
Œ¶Łș90·Ö~100·ÖŁ»![]() Œ¶Łș75·Ö~89·ÖŁ»
Œ¶Łș75·Ö~89·ÖŁ»![]() Œ¶60·Ö~74·ÖŁ»
Œ¶60·Ö~74·ÖŁ»![]() Œ¶Łș60·ÖÒÔÏÂŁ©
Œ¶Łș60·ÖÒÔÏÂŁ©
Łš1Ł©ŽËŽÎłéŃùčČ”śČéÁ˶àÉÙĂûѧÉúŁż
Łš2Ł©ÇëÇółöŃù±ŸÖĐ![]() Œ¶”ÄѧÉúÈËÊ꣏ŸźČčÈ«ÌőĐÎÍłŒÆÍŒŁ»
Œ¶”ÄѧÉúÈËÊ꣏ŸźČčÈ«ÌőĐÎÍłŒÆÍŒŁ»
Łš3Ł©ÈôžĂĐŁŸĆÄꌶÓĐ1000ĂûѧÉúŁŹÇëÄăÓĂŽËŃù±ŸčÀŒÆÒŐÊőČâÊÔÖĐ·ÖÊęČ»”ÍÓÚ75·Ö”ÄѧÉúÈËÊ꣏
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com