
【题目】一次函数y1=kx+b与反比例函数y2=![]() (n>0)交于点A(1,3),B(3,m).
(n>0)交于点A(1,3),B(3,m).
(1)分别求两个函数的解析式;
(2)根据图像直接写出,当x为何值时,y1<y2;
(3)在x轴上找一点P,使得△OAP的面积为6,求出P点坐标.
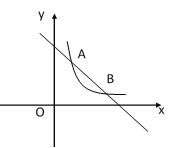
【答案】(1)y2=![]() ,y1=-x+4.(2)x<1或x>3.(3)(-4,0)或(4,0).
,y1=-x+4.(2)x<1或x>3.(3)(-4,0)或(4,0).
【解析】
(1)首先将A,B两点坐标代入反比例函数解析式,得出m,n的值,在利用待定系数法即可解决问题;
(2)观察图象,写出一次函数的图象在反比例函数图象下方时,x的取值范围即可;
(3)由题意可知A的纵坐标的值即为△OAP的高,且P点在横轴上,根据三角形的面积公式可知OP的长为4,写出可能的坐标即可.
解:(1)将A(1,3),代入y2=![]() (n>0),得n=3,
(n>0),得n=3,
再将B(3,m)代入y2=![]() ,得m=1,
,得m=1,
所以将A,B两点坐标代入y1=kx+b,
得![]() ,
,
解得![]() ,
,
∴一次函数解析式为y1=-x+4;
(2)根据题意的一次函数的图象在反比例函数图象下方时所对应的x的取值范围即为所求,此时x的范围是:x<1或x>3;
(3)由题意得△OAP的高为3
∴S△OAP=![]() ·3·|OP|=6,
·3·|OP|=6,
∴OP的长为4,
又∵点P在x轴上,
∴点P的坐标为(-4,0)或(4,0).


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A.概率是1%的事件在一次试验中一定不会发生
B.要了解某公司生产的100万只灯泡的使用寿命,可以采用全面调查的方式
C.甲乙两人各自跳远10次,若他们跳远成绩的平均数相同,甲乙跳远成绩的方差分别为0.51和0.62,则乙的成绩更稳定
D.随意翻到一本书的某页,页码是奇数是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10![]() km,一艘货轮从B港口沿如图所示的BC方向航行4
km,一艘货轮从B港口沿如图所示的BC方向航行4![]() km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.

A.8![]() B.9
B.9![]() C.6
C.6![]() D.7
D.7![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济宁某校为了解九年级学生艺术测试情况.以九年极(1)班学生的艺术测试成绩为样本,按![]() 、
、![]() 、
、![]() 、
、![]() 四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:
四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:

(说明:![]() 级:90分~100分;
级:90分~100分;![]() 级:75分~89分;
级:75分~89分;![]() 级60分~74分;
级60分~74分;![]() 级:60分以下)
级:60分以下)
(1)此次抽样共调查了多少名学生?
(2)请求出样本中![]() 级的学生人数,井补全条形统计图;
级的学生人数,井补全条形统计图;
(3)若该校九年级有1000名学生,请你用此样本估计艺术测试中分数不低于75分的学生人数,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个边长为4的正方形![]() 分割成如图所示的9部分,其中
分割成如图所示的9部分,其中![]() ,
,![]() ,
,![]() ,
,![]() 全等,
全等,![]() ,
,![]() ,
,![]() ,
,![]() 也全等,中间小正方形
也全等,中间小正方形![]() 的面积与
的面积与![]() 面积相等,且
面积相等,且![]() 是以
是以![]() 为底的等腰三角形,则
为底的等腰三角形,则![]() 的面积为( )
的面积为( )
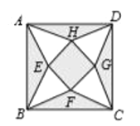
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (
(![]() 为常数)与
为常数)与![]() 轴交于点
轴交于点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点.
为抛物线顶点.
(Ⅰ)当![]() 时,求点
时,求点![]() ,点
,点![]() 的坐标;
的坐标;
(Ⅱ)①若顶点![]() 在直线
在直线![]() 上时,用含有
上时,用含有![]() 的代数式表示
的代数式表示![]() ;
;
②在①的前提下,当点![]() 的位置最高时,求抛物线的解析式;
的位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求
值最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
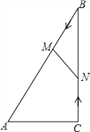
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com