
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=5cm����BAC=60��������M�ӵ�B��������BA������ÿ��2cm���ٶ����A�����˶���ͬʱ����N�ӵ�C��������CB������ÿ��![]() cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
cm���ٶ����B�����˶������˶�ʱ��Ϊt�루0��t��5��������MN��
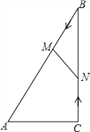
��1����BM=BN����t��ֵ��
��2������MBN���ABC���ƣ���t��ֵ��
��3����tΪ��ֵʱ���ı���ACNM�������С���������Сֵ��
���𰸡���1��10![]() -15����2��t=
-15����2��t=![]() ��t=
��t=![]() ����3��t=2.5����СֵΪ
����3��t=2.5����СֵΪ![]()
�������������������1������Rt��ABC�����ʵó�AB��BC�ij��ȣ�Ȼ�����BM=BN�ó�t��ֵ����2������MBN�ס�ABC����NBM�ס�ABC��������ֱ����t��ֵ����3�������ı��ε����������ABC�������ȥ��BMN������ó���������ʽ���Ӷ������ֵ.
�����������1������Rt��ABC����ACB=90����AC=5����BAC=60������![]() ��
��![]()
������֪![]() ��
��![]() ��
��![]() �� ��BM=BN��
�� ��BM=BN��![]()
��ã�![]()
��2��������MBN�ס�ABCʱ�� ��![]() ����
����![]() ����ã�
����ã�![]()
������NBM�ס�ABCʱ�� ��![]() �� ��
�� ��![]() ����ã�
����ã�![]() ��
��
����![]() ��
��![]() ʱ����MBN����ABC���ƣ�
ʱ����MBN����ABC���ƣ�
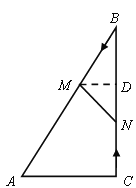
��3����M��MD��BC�ڵ�D���ɵã�![]() ���ı���ACNM�����Ϊ
���ı���ACNM�����Ϊ![]() ��
��
��![]()
![]()
![]()
![]() ��
��
�����ݶ��κ��������ʿ�֪����![]() ʱ��
ʱ��![]() ��ֵ��С�� ��ʱ��
��ֵ��С�� ��ʱ��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ίԱ����500ԪǮȥ��������Ʒ����֪һ������aԪ��һ������bԪ�������ʽ500��3a��2b��ʾ������Ϊ___________________________________________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У���һ��ֱ���������Ĵ��ߣ�����������Χ�ɾ��ε��ܳ����������������ȣ�������������г�㣮
��1���жϵ�M����1��2����N����4����4���Ƿ�Ϊ��г�㣬��˵�����ɣ�
��2������г��P��a��3����ֱ��y=��x+b��bΪ�������ϣ�����a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ�AB�ǡ�O��ֱ����OD��AB�ڵ�O���ֱ�AC��CF�ڵ�E��D����DE=DC��

��1����֤��CF�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ5��BC=![]() ����DE�ij���
����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�AB=12��CD=6���߶�CD��ֱ��AB���˶���A��B����࣬C��D����ࣩ��
��1����D����B���غ�ʱ��AC=_________��
��2����P���߶�AB�ӳ���������һ�㣬�ڣ�1���������£���PA+PB�C2PC��ֵ��
��3��M��N�ֱ���AC��BD���е㣬��BC=4ʱ����MN�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ2018���������300��Ԫ����2020����ƻ�����ﵽ507��Ԫ.���������������ƽ��������Ϊx.Ӧ�з����ǣ� ��
A. 300��1+x��=507 B. 300��1+x��2=507
C. 300��1+x��+300��1+x��2=507 D. 300+300��1+x��+300��1+x��2=507
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���öȡ��֡����ʾ91.34��Ϊ��������
A. 91��20'24' B. 91��34' C. 91��20'4' D. 91��3'4'
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ֽ���ʽa4��2a2+1�Ľ���ǣ�������
A. ��a2+1��2 B. ��a2��1��2 C. a2��a2��2�� D. ��a+1��2��a��1��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com