
【题目】如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.

(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为5,BC=![]() ,求DE的长.
,求DE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OC,欲证明CF是⊙O的切线,只要证明∠OCF=90°.
(2)作DH⊥AC于H,由△AEO∽△ABC,得![]() 求出AE,EC,再根据sin∠A=sin∠EDH,得到
求出AE,EC,再根据sin∠A=sin∠EDH,得到![]() ,求出DE即可.
,求出DE即可.
试题解析:连接OC,∵OA=OC,∴∠A=∠OCA,∵OD⊥AB,∴∠A+∠AEO=90°,∵DE=DC,∴∠DEC=∠DCE,∵∠AEO=∠DCE,∴∠AEO=∠DCE,∴∠OCE+∠DCE=90°,∠OCF=90°,∴OC⊥CF,∴CF是⊙O切线.
(2)作DH⊥AC于H,则∠EDH=∠A,∵DE=DC,∴EH=HC=![]() EC,∵⊙O的半径为5,BC=
EC,∵⊙O的半径为5,BC=![]() ,∴AB=10,AC=
,∴AB=10,AC=![]() ,∵△AEO∽△ABC,∴
,∵△AEO∽△ABC,∴![]() ,∴AE=
,∴AE=![]() ,∴EC=AC﹣AE=
,∴EC=AC﹣AE=![]() ,∴EH=
,∴EH=![]() EC=
EC=![]() ,∵∠EDH=∠A,∴sin∠A=sin∠EDH,∴
,∵∠EDH=∠A,∴sin∠A=sin∠EDH,∴![]() ,∴DE=
,∴DE=![]() =
= =
=![]() .
.



 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为________;
②该函数的一条性质:__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(﹣4,4),点B的坐标为(0,1).以点A为直角顶点作∠CAD=90°,射线AC交y轴的负半轴于点C,射线AD交x轴的负半轴于点D.
(1)求直线AB的解析式;
(2)OD﹣OC的值是否为定值?如果是,求出它的值;如果不是,求出它的变化范围;
(3)平面内存在点P,使得A、B、C、P四点能构成菱形,
①P点坐标为 ;
②点Q是射线AC上的动点,求PQ+DQ的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每组数分别是三根木棒的长度,能用它们摆成三角形的是( )
A.3cm,4cm,8cm
B.8cm,7cm,15cm
C.5cm,5cm,11cm
D.13cm,12cm,20cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?
查看答案和解析>>
科目:初中数学 来源: 题型:
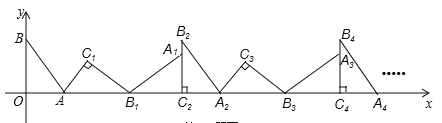
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
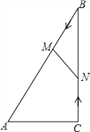
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 画一条3厘米长的射线 B. 画一条3厘米长的直线
C. 画一条5厘米长的线段 D. 在线段、射线、直线中直线最长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com