
����Ŀ����ͼ����A������Ϊ����4��4������B������Ϊ��0��1�����Ե�AΪֱ�Ƕ�������CAD=90��������AC��y��ĸ������ڵ�C������AD��x��ĸ������ڵ�D��
��1����ֱ��AB�Ľ���ʽ��
��2��OD��OC��ֵ�Ƿ�Ϊ��ֵ������ǣ��������ֵ��������ǣ�������ı仯��Χ��
��3��ƽ���ڴ��ڵ�P��ʹ��A��B��C��P�ĵ��ܹ������Σ�
��P������Ϊ ��
�ڵ�Q������AC�ϵĶ��㣬��PQ+DQ����Сֵ��

���𰸡��⣺(1) y=![]() x+1
x+1
(2) �Ƕ�ֵ��OD-OC=8��
(3) �٣�-4��-1�� ��PQ+DQ����СֵΪ![]()
���������⣺��1����ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0�����ߵ�A����4��4������B��0��1����ֱ��AB�ϣ���![]() ����ã�
����ã� 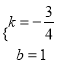 ����ֱ��AB�Ľ���ʽΪ��
����ֱ��AB�Ľ���ʽΪ�� ![]() ��
��
��2���Ƕ�ֵ���������£�
����A�ֱ���x�ᣬy��Ĵ��ߣ�����ֱ�ΪE��F�����ͼ�����ɵá�AED=��AFC=90�㣬�֡ߡ�BOD=90�㣬���EAF=90�㣬����CAE+��CAF=90�㣬�ߡ�CAD=90�㣬����CAE+��DAE=90�㣬���DAE=��CAF����A����4��4������OE=AF=AE=OF=4���ڡ�AED�͡�AFC�У��ߡ�DAE=��CAF��AE=AF����AED=��AFC=90�㣬���AED�ա�AFC��ASA������ED=FC����OD��OC=��OE+ED������FC��OF��=OE+OF=8����OD��OC��ֵ�������仯��ֵΪ8��

��3���������εĶԽ����ഹֱ����AB��BC��Ȼ�����ܴ�ֱ����AB��BCֻ�����ڱߣ���AB=![]() =5����BC=5����C��0��-4������P��x��y�����������ζԽ�����ƽ�ֺ��е����깫ʽ�У�
=5����BC=5����C��0��-4������P��x��y�����������ζԽ�����ƽ�ֺ��е����깫ʽ�У� ![]() ��
�� ![]() ����ã�x=-4��y=-1����P��-4��-1����
����ã�x=-4��y=-1����P��-4��-1����
�ڡ�����ABCP�У�B��P����AC�Գ��� ��PQ=BQ�� ����PQ+DQ��min=��BQ+DQ��min=BD
��BC=BA=5����OC=4
����2���ã�OD=OC+8=12�� ��Rt��BOD���� ![]()
��PQ+DQ����СֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ĸ����⣺����ȵĽ��ǶԶ��ǣ���ͬλ����ȣ�������֮�䣬ֱ����̣��ܴ�ֱ����һ�㵽����ֱ�ߵĴ��߶Σ������㵽ֱ�ߵľ��룮������������ĸ����У�������
A. 0�� B. 1�� C. 2�� D. 3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ίԱ����500ԪǮȥ��������Ʒ����֪һ������aԪ��һ������bԪ�������ʽ500��3a��2b��ʾ������Ϊ___________________________________________________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ����ҹ�����ĸ002���㲿����������ĵ��飬���ʺϲ��õĵ��鷽ʽ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ڵ�����ֱ�����ཻ��ƽ������λ�ù�ϵ��
��1����ͼ1����AB��CD����P��AB��CD�ⲿ�����С�B=��BOD�������BOD�ǡ�POD����ǣ��ʡ�BOD=��BPD+��D���á�BPD=��B����D������P�Ƶ�AB��CD�ڲ�����ͼ2�����Ͻ����Ƿ��������������˵�����ɣ��������������BPD����B����D֮���к�������ϵ����֤����Ľ��ۣ�
��2������ͼ2�У���ֱ��AB�Ƶ�B��ʱ�뷽����תһ���ǶȽ�ֱ��CD�ڵ�Q����ͼ3�����BPD����B����D����BQD֮���к�������ϵ��������֤������
��3�����ݣ�2���Ľ�������ͼ4�С�A+��B+��C+��D+��E�Ķ�����
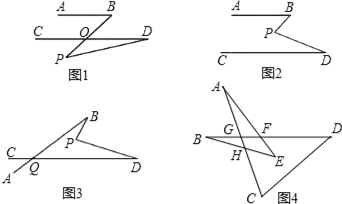
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ƽ��ֱ������ϵ�У���һ��ֱ���������Ĵ��ߣ�����������Χ�ɾ��ε��ܳ����������������ȣ�������������г�㣮
��1���жϵ�M����1��2����N����4����4���Ƿ�Ϊ��г�㣬��˵�����ɣ�
��2������г��P��a��3����ֱ��y=��x+b��bΪ�������ϣ�����a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǡ�O���ڽ������Σ�AB�ǡ�O��ֱ����OD��AB�ڵ�O���ֱ�AC��CF�ڵ�E��D����DE=DC��

��1����֤��CF�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ5��BC=![]() ����DE�ij���
����DE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com