
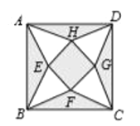
【题目】将一个边长为4的正方形![]() 分割成如图所示的9部分,其中
分割成如图所示的9部分,其中![]() ,
,![]() ,
,![]() ,
,![]() 全等,
全等,![]() ,
,![]() ,
,![]() ,
,![]() 也全等,中间小正方形
也全等,中间小正方形![]() 的面积与
的面积与![]() 面积相等,且
面积相等,且![]() 是以
是以![]() 为底的等腰三角形,则
为底的等腰三角形,则![]() 的面积为( )
的面积为( )
A.2B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】一水果店主分两批购进同一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果每箱的单价是多少元?
(2)该水果店主计划两批水果的售价均定为每千克4元,每箱10千克,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了2%的损耗,但这两批水果销售完后仍赚了不低于2346元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
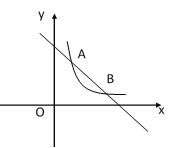
【题目】一次函数y1=kx+b与反比例函数y2=![]() (n>0)交于点A(1,3),B(3,m).
(n>0)交于点A(1,3),B(3,m).
(1)分别求两个函数的解析式;
(2)根据图像直接写出,当x为何值时,y1<y2;
(3)在x轴上找一点P,使得△OAP的面积为6,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
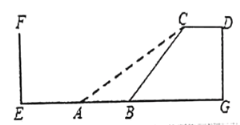
【题目】速滑运动受到许多年轻人的喜爱。如图,四边形![]() 是某速滑场馆建造的滑台,已知
是某速滑场馆建造的滑台,已知![]() ,滑台的高
,滑台的高![]() 为
为![]() 米,且坡面
米,且坡面![]() 的坡度为
的坡度为![]() .后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为
.后来为了提高安全性,决定降低坡度,改造后的新坡面AC的坡度为![]() .
.
(1)求新坡面![]() 的坡角及
的坡角及![]() 的长;
的长;
(2)原坡面底部![]() 的正前方
的正前方![]() 米处
米处![]() 是护墙
是护墙![]() ,为保证安全,体育管理部门规定,坡面底部至少距护墙
,为保证安全,体育管理部门规定,坡面底部至少距护墙![]() 米。请问新的设计方案能否通过,试说明理由(参考数据:
米。请问新的设计方案能否通过,试说明理由(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
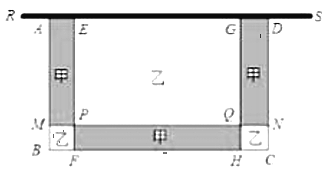
【题目】某校一面墙![]() 前有一块空地,校方准备用长
前有一块空地,校方准备用长![]() 的栅栏(
的栅栏(![]() )围成一个一面靠墙的长方形花围,再将长方形
)围成一个一面靠墙的长方形花围,再将长方形![]() 分割成六块(如图所示) ,已知
分割成六块(如图所示) ,已知![]() ,
,![]() ,
,![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示:
的代数式表示:![]() ;
;![]() .
.
(2)当长方形![]() 的面积等于
的面积等于![]() 时,求
时,求![]() 的长.
的长.
(3)若在如图的甲区域种植花卉.乙区域种柏草坪,种柏花卉的成本为每平方米100元,种被草坪的成本为每平方米50元,若种植花卉与草坪的总费用超过6300元,求花围的宽![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 有两个不同的交点.下列结论:①
有两个不同的交点.下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则
有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
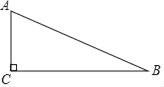
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=1,tan∠CAB=2,将△ABC绕点A旋转后,点B落在AC的延长线上的点D,点C落在点E,DE与直线BC相交于点F,那么CF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com