
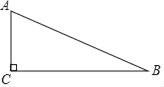
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=1,tan∠CAB=2,将△ABC绕点A旋转后,点B落在AC的延长线上的点D,点C落在点E,DE与直线BC相交于点F,那么CF=_____.
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
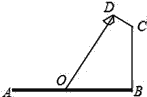
【题目】如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD=![]() 米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
米,则路灯的灯柱BC高度应该设计为____米(计算结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处与灯塔P的距离约为_______nmile.(结果取整数,参考数据:![]() =1.7,
=1.7, ![]() ≈ 1.4)
≈ 1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 y=ax2﹣5ax+c 交 x 轴于点 A,点 A 的坐标为(4,0).
(1)用含 a 的代数式表示 c.
(2)当 a=![]() 时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
(3)当 a=![]() 时,求 0≤x≤6 时 y 的取值范围.
时,求 0≤x≤6 时 y 的取值范围.
(4)已知点 B 的坐标为(0,3),当抛物线的顶点落在△AOB 外接圆内部时,直接写出 a的取值范围.
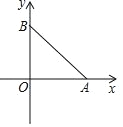
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将抛物线y=﹣x2平移后经过点A(﹣1,0)、B(4,0),且平移后的抛物线与y轴交于点C(如图).
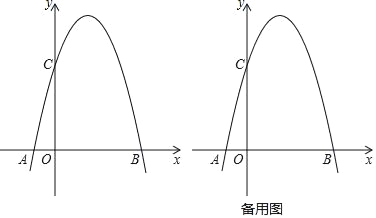
(1)求平移后的抛物线的表达式;
(2)如果点D在线段CB上,且CD=![]() ,求∠CAD的正弦值;
,求∠CAD的正弦值;
(3)点E在y轴上且位于点C的上方,点P在直线BC上,点Q在平移后的抛物线上,如果四边形ECPQ是菱形,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.
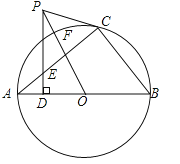
(1)求证:PC是⊙O的切线;
(2)若PC=3,PF=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
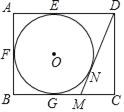
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于点E、F、G,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求化简:(a﹣1)÷![]() ,并选择你喜欢的整数a,b代入求值.
,并选择你喜欢的整数a,b代入求值.
小聪计算这一题的过程如下:
解:原式=(a﹣1)÷![]() …①
…①
=(a﹣1)![]() …②
…②
=![]() …③
…③
当a=1,b=1时,原式=![]() …④
…④
以上过程有两处关键性错误,第一次出错在第_____步(填序号),原因:_____;
还有第_____步出错(填序号),原因:_____.
请你写出此题的正确解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com