
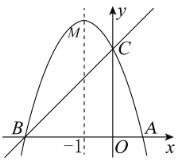
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
【答案】(1)抛物线的解析式为![]() ,直线的解析式为
,直线的解析式为![]() .(2)
.(2)![]() ;(3)
;(3)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
(1)依题意得: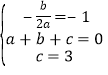 ,解得:
,解得: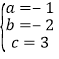 ,
,
∴抛物线的解析式为![]() .
.
∵对称轴为![]() ,且抛物线经过
,且抛物线经过![]() ,
,
∴把![]() 、
、![]() 分别代入直线
分别代入直线![]() ,
,
得![]() ,解之得:
,解之得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)直线![]() 与对称轴
与对称轴![]() 的交点为
的交点为![]() ,则此时
,则此时![]() 的值最小,把
的值最小,把![]() 代入直线
代入直线![]() 得
得![]() ,
,
∴![]() .即当点
.即当点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小时
的距离之和最小时![]() 的坐标为
的坐标为![]() .
.
(注:本题只求![]() 坐标没说要求证明为何此时
坐标没说要求证明为何此时![]() 的值最小,所以答案未证明
的值最小,所以答案未证明![]() 的值最小的原因).
的值最小的原因).
(3)设![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
①若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:![]() ,
,
②若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:![]() ,
,
③若点![]() 为直角顶点,则
为直角顶点,则![]() ,即:
,即:![]() 解得:
解得:
![]() ,
,![]() .
.
综上所述![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).
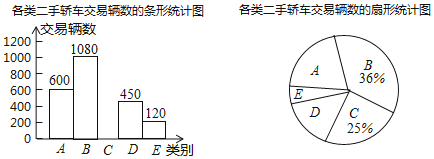
请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
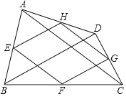
【题目】如图,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是四边形
分别是四边形![]() 边
边![]() 、
、![]() 、
、![]() 、
、![]() 的中点.则下列说法:①若
的中点.则下列说法:①若![]() ,则四边形
,则四边形![]() 为矩形;②若
为矩形;②若![]() ,则四边形
,则四边形![]() 为菱形;③若四边形
为菱形;③若四边形![]() 是平行四边形,则
是平行四边形,则![]() 与
与![]() 互相平分;④若四边形
互相平分;④若四边形![]() 是正方形,则
是正方形,则![]() 与
与![]() 互相垂直且相等.其中正确的个数是( )
互相垂直且相等.其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包荒山若干亩,种果树![]() 棵,今年水果总产量为
棵,今年水果总产量为![]() 千克.目前有两种销售方式:一、此水果在市场上每千克售
千克.目前有两种销售方式:一、此水果在市场上每千克售![]() 元,该农户将水果拉到市场出售平均每天出售
元,该农户将水果拉到市场出售平均每天出售![]() 千克,需
千克,需![]() 人帮忙,每人每天需付工资
人帮忙,每人每天需付工资![]() 元,农用车运费及其他各项税费平均每天
元,农用车运费及其他各项税费平均每天![]() 元.二、 直接在果园每千克售
元.二、 直接在果园每千克售![]() 元
元![]() .
.
(1)分别用![]() 表示两种方式出售水果的收入.
表示两种方式出售水果的收入.
(2)若![]() 元,
元,![]() 元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
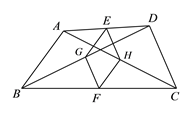
【题目】如图,在四边形ABCD中,AB=DC,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点.
(1)求证:四边形EGFH是菱形;
(2)若AB=4,且BA、CD延长后相交所成的锐角是60°,求四边形EGFH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
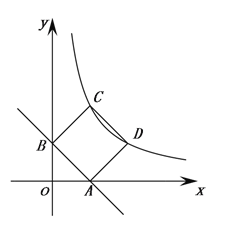
【题目】如图:一次函数y=kx+b的图像交x轴正半轴于点A、y轴正半轴于点B,且OA=OB=1.以线段AB为边在第一象限作正方形ABCD,点D在反比例函数y=![]() 图像上.
图像上.
(1)求一次函数的关系式,并判断点C是否在反比例函数y=![]() 图像上;
图像上;
(2)在直线AB上找一点P,使PC+PD的值最小,并求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN为一电视塔,AB是坡角为30°的小山坡(电视塔的底部N与山坡的坡脚A在同一水平线上,被一个人工湖隔开),某数学兴趣小组准备测量这座电视塔的高度.在坡脚A处测得塔顶M的仰角为45°;沿着山坡向上行走40m到达C处,此时测得塔顶M的仰角为30°,请求出电视塔MN的高度.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 为原点,点
为原点,点![]() 及在第一象限的动点
及在第一象限的动点![]() ,且
,且![]() ,设
,设![]() 的面积为
的面积为![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 点坐标;
点坐标;
(4)画出函数![]() 的图象.
的图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com