
【题目】如图,点![]() 、
、![]() 、
、![]() 、
、![]() 分别是四边形
分别是四边形![]() 边
边![]() 、
、![]() 、
、![]() 、
、![]() 的中点.则下列说法:①若
的中点.则下列说法:①若![]() ,则四边形
,则四边形![]() 为矩形;②若
为矩形;②若![]() ,则四边形
,则四边形![]() 为菱形;③若四边形
为菱形;③若四边形![]() 是平行四边形,则
是平行四边形,则![]() 与
与![]() 互相平分;④若四边形
互相平分;④若四边形![]() 是正方形,则
是正方形,则![]() 与
与![]() 互相垂直且相等.其中正确的个数是( )
互相垂直且相等.其中正确的个数是( )
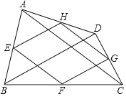
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】
因为一般四边形的中点四边形是平行四边形,当对角线BD=AC时,中点四边形是菱形,当对角线AC⊥BD时,中点四边形是矩形,当对角线AC=BD,且AC⊥BD时,中点四边形是正方形,
解:
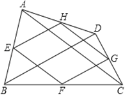
∵点![]() 、
、![]() 、
、![]() 、
、![]() 分别是四边形
分别是四边形![]() 边
边![]() 、
、![]() 、
、![]() 、
、![]() 的中点,
的中点,
∴EH![]()
![]() BD,FG
BD,FG![]()
![]() BD, HG
BD, HG![]()
![]() AC,EF
AC,EF![]()
![]() AC,
AC,
∴EH![]() FG ,
FG ,
∴四边形EFGH为平行四边形.
①若AC=BD时,
∵EH=![]() BD,HG=
BD,HG=![]() AC,
AC,
∴EH=HG,
∴平行四边形EFGH为菱形。序号①错误.
②若![]() ,
,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH为矩形。序号②错误.
③若四边形![]() 是平行四边形时,如图,AC,BD不互相平分。序号③错误.
是平行四边形时,如图,AC,BD不互相平分。序号③错误.
④若四边形![]() 是正方形,
是正方形,
则EH⊥HG,EH=HG,
又∵EH![]()
![]() BD,HG
BD,HG![]()
![]() AC,
AC,
∴AC⊥BD,AC=BD.∴序号④正确.
故选:A.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】某超市在“元旦”期间对顾客实行优惠,规定一次性购物优惠办法:
少于200元,不予优惠;高于200元但低于500元时,九折优惠;消费500元或超过500元时,其中500元部分给予九折优惠,超过500元部分给予八折优惠.根据优惠条件完成下列任务:
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款0.9x,当x大于或等于500元时,他实际付款多少元?(用含x的代数式表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的式子表示王老师两次购物实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
(发现与证明)![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() ,连结
,连结![]() .
.
结论1:![]() 与
与![]() 重叠部分的图形是等腰三角形;
重叠部分的图形是等腰三角形;
结论2:![]() .
.
试证明以上结论.
(应用与探究)
在![]() 中,已知
中,已知![]() ,
,![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() ,连结
,连结![]() .若以
.若以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是正方形,求
为顶点的四边形是正方形,求![]() 的长.(要求画出图形)
的长.(要求画出图形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程,小明离家的距离![]() 与时间
与时间![]() 之间的对应关系.根据图象,下列说法中正确的是( )
之间的对应关系.根据图象,下列说法中正确的是( )
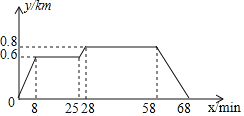
A. 小明吃早餐用了25分钟
B. 食堂到图书馆的距离为![]()
C. 小明读报用了30分钟
D. 小明从图书馆回家的平均速度为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有6个质地和大小均相同的球,每个球只标有一个数字,将标有3,4,5的三个球放入甲箱中,标有4,5,6的三个球放入乙箱中.
(1)小宇从甲箱中随机模出一个球,求“摸出标有数字是3的球”的概率;
(2)小宇从甲箱中、小静从乙箱中各自随机摸出一个球,若小宇所摸球上的数字比小静所摸球上的数字大1,则称小宇“略胜一筹”.请你用列表法(或画树状图)求小宇“略胜一筹”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,点
,点![]() 是线段
是线段![]() 的中点,先按要求画图形,再解决问题.
的中点,先按要求画图形,再解决问题.
(1)延长线段![]() 至点
至点![]() ,使
,使![]() ;延长线段
;延长线段![]() 至点
至点![]() ,使
,使![]() ;(尺规作图,保留作图痕迹)
;(尺规作图,保留作图痕迹)
(2)求线段![]() 的长度;
的长度;
(3)若点![]() 是线段
是线段![]() 的中点,求线段
的中点,求线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校8千米的某地参加社会实践活动,一部分同学步行,另一部分同学骑自行车,沿相同路线前往.如图,![]() ,
,![]() 分别表示步行和骑车的同学前往目的地所走的路程
分别表示步行和骑车的同学前往目的地所走的路程![]() (千米)与所用时间
(千米)与所用时间![]() (分钟)之间的函数图象.则下列判断错误的是( )
(分钟)之间的函数图象.则下列判断错误的是( )
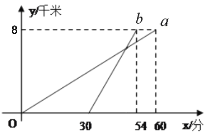
A. 骑车的同学比步行的同学晚出发30分钟
B. 骑车的同学和步行的同学同时到达目的地
C. 步行的速度是7.5千米/小时
D. 骑车的同学从出发到追上步行的同学用了18分钟
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com