
����Ŀ��������һ�����⣺̽��ͬһƽ��ֱ������ϵ��ϵ����Ϊ��������������������![]() ��
��![]() ��k��0����ͼ�����ʣ�
��k��0����ͼ�����ʣ�
С������ѧϰ�����ľ��飬�Ժ���![]() ��
��![]() ��k��0������k��0ʱ��ͼ�����ʽ�����̽����
��k��0������k��0ʱ��ͼ�����ʽ�����̽����
������С����̽�����̣�
��1����ͼ��ʾ���躯��![]() ��
��![]() ͼ��Ľ���ΪA��B����֪A�������Ϊ����k����1������B�������Ϊ�� ����
ͼ��Ľ���ΪA��B����֪A�������Ϊ����k����1������B�������Ϊ�� ����
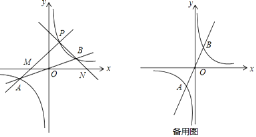
��2������PΪ��һ������˫��������ͬ�ڵ�B������һ�㣮
����ֱ��PA��x���ڵ�M��ֱ��PB��x���ڵ�N����֤��PM=PN��
֤���������£���P��m��![]() ����ֱ��PA�Ľ���ʽΪy=ax+b��a��0����
����ֱ��PA�Ľ���ʽΪy=ax+b��a��0����
��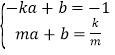 ����ã�
����ã�![]() ��
��
��ֱ��PA�Ľ���ʽΪ�� ��.
���������Ľ����̲��������������ʣ���֤����
�ڵ�P������Ϊ��1��k����k��1��ʱ���ж���PAB����״������k��ʾ����PAB�������
���𰸡�(1) B��k��1��;(2)�ټ�����;��1��k2.
��������
��1��������������������ͼ��ĶԳ��Խ�ϵ�A�����꼴�ɵó���B�����ꣻ
��2������![]() �����ݵ�P��A���������ô���ϵ���������ֱ��PA�Ľ���ʽ������һ�κ���ͼ���ϵ�����������������M�����꣬����P��PH��x����H���ɵ�P������ɵó���H�����꣬�����������MH�ij��ȣ�ͬ���ɵó�HN�ij��ȣ��ٸ��ݵ��������ε����ߺ�һ����֤��PM=PN��
�����ݵ�P��A���������ô���ϵ���������ֱ��PA�Ľ���ʽ������һ�κ���ͼ���ϵ�����������������M�����꣬����P��PH��x����H���ɵ�P������ɵó���H�����꣬�����������MH�ij��ȣ�ͬ���ɵó�HN�ij��ȣ��ٸ��ݵ��������ε����ߺ�һ����֤��PM=PN��
�ڸ��ݢٽ��PH��MH��NH�ij��ȣ��ɵó���PABΪֱ�������Σ���k>1��0<k<1������������÷ָ�ͼ������������������PAB�������
(1)����������������ͼ��ĶԳ��Կ�֪����A. B����ԭ��O�Գƣ�
��A�������Ϊ(k,1)��
��B�������Ϊ(k,1).
�ʴ�Ϊ��(k,1).
��2��)��֤����������,��![]() ,ֱ��PA�Ľ���ʽΪy=ax+b(a��0).
,ֱ��PA�Ľ���ʽΪy=ax+b(a��0).
��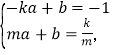
��ã� 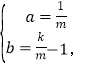
��ֱ��PA�Ľ���ʽΪ![]()
��y=0ʱ��x=mk��
��M�������Ϊ(mk,0).
����P��PH��x����H����ͼ1��ʾ��
��P������Ϊ![]() ��
��
��H���������m��0����
��MH=xH��xM=m����m��k��=k��
ͬ���ɵã�HN=k��
��MH=HN����PM=PN��
���ɢٿ�֪������PMN�У�PM=PN�����PMNΪ���������Σ���MH=HN=k��
��P������Ϊ��1��k��ʱ��PH=k����MH=HN=PH��
���PMH=��MPH=45������PNH=��NPH=45����
���MPN=90��������APB=90�������PABΪֱ�������Σ�
��k��1ʱ����ͼ1��
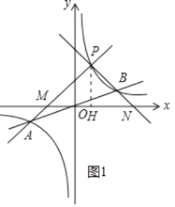
S��PAB=S��PMN��S��OBN+S��OAM��
=![]() MNPH��
MNPH��![]() ONyB+
ONyB+![]() OM|yA|��
OM|yA|��
=![]() ��2k��k��
��2k��k��![]() ��k+1����1+
��k+1����1+![]() ��k��1����1��
��k��1����1��
=k2��1��
��0��k��1ʱ����ͼ2��
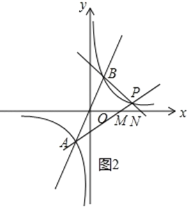
S��PAB=S��OBN��S��PMN+S��OAM��
=![]() ONyB��k2+
ONyB��k2+![]() OM|yA|��
OM|yA|��
=![]() ��k+1����1��k2+
��k+1����1��k2+![]() ��1��k����1��
��1��k����1��
=1��k2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��һ��ת�̱��ֳ�6����ȵ�����,��ɫ��Ϊ�졢�̡�������,ָ���λ�ù̶�,ת��ת�̺���������ֹͣ,���е�ij�����λ�ǡ��ͣ��ָ����ָ��λ��(ָ��ָ���������εĽ���ʱ,����ת��).�����¼�:��ָ��ָ���ɫ;��ָ��ָ����ɫ;(��ָ��ָ���ɫ;��ָ�벻ָ���ɫ,���Ƹ��¼��Ŀ����Դ�С,�����������.
(1)���¼������Ŀ����Դ�С�� ��
(2)���ʵ��,ָ��ָ����ɫ��Ƶ�ʵĹ���ֵ�� ��
(3)����Щ�¼�����Ű������Ŀ����Դ�С�����˳������Ϊ: ![]()
![]()
![]() .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶Ϊ1��ֱ��CD����Բ��O������O��C��D���㣬ֱ��AB��CD����M��ֱ��CD�����ڵ�C��O��D��һ�����㣬AM���ڵ�ֱ�߽��ڡ�O�ڵ�N����P��ֱ��CD����һ�㣬��PM=PN��
��1������M�ڡ�O�ڲ�����ͼһ�����ж�PN���O�Ĺ�ϵ����д��֤�����̣�
��2������M�ڡ�O�ⲿ����ͼ����������������ʱ����1���Ľ����Ƿ�������˵�����ɣ�
��3������M�ڡ�O�ⲿ����ͼ������AMO=15������ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ, ��֪A��-4��-1����B��-5��-4����C��-1��-3������ABC����ƽ�Ƶõ��ġ�A��B��C��,��ABC������һ��P(x1,y1)ƽ�ƺ�Ķ�Ӧ��ΪP��(x1+6,y1+4)��
��1������ͼ��������A��B��C�䣻��2��д����A�䡢B�䡢C�������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD����M�DZ�BA�ӳ����ϵĶ��㣨�����A�غϣ�����AM��AB����CBE����DAMƽ�Ƶõ���������E��EH��AC��HΪ���㣬�������½��ۣ�����Mλ�ñ仯��ʹ����DHC=60��ʱ��2BE=DM�������۵�M�˶����δ�������DM=![]() HM�������۵�M�˶����δ�����CHMһ������135�㣮������ȷ���۵����Ϊ_____��
HM�������۵�M�˶����δ�����CHMһ������135�㣮������ȷ���۵����Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:����ABC�У��ҡ�BAC��70����AD����ABC�Ľ�ƽ���ߣ���E��AC���ϵ�һ�㣬��FΪֱ��AB�ϵ�һ���㣬����EF��ֱ��EF��ֱ��AD���ڵ�P�����AEF������
(1)��ͼ�٣��� DE//AB����١�ADE�Ķ�����_______;
�ڵ���DPE����DEPʱ����AEF= _____��:����PDE����PED����AEF=_______��;
(2)��ͼ�ڣ���DE��AC�����Ƿ��������������ֵ��ʹ����DPE����������ȵĽ�?�������������ֵ;�������ڣ�˵������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱߡ�OAB�͵ȱߡ�AFE��һ�߶���x���ϣ�˫����y=![]() ��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��
��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��
��1�����˫��������ʾ�ĺ�������ʽ��
��2����ȱߡ�AEF�ı߳���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c(a��0)��ͼ����x�ύ��A��B���㣬��y�ύ��C�㣬�ҶԳ���Ϊֱ��x=1����B����Ϊ(��1��0)����������ĸ����ۣ���2a+b=0����4a��2b+c��0����ac��0���ܵ�y��0ʱ��x����1��x��3��������ȷ�ĸ����ǣ� ��

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ı���![]() �У��Խ���
�У��Խ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ����
����![]() ��������
��������![]() ��
��![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() .
.

��1����ͼ�е�ͼ1����֤��![]() ��
��
��2����ͼ�е�ͼ2��![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() ���ڲ������κθ����ߵ�����£����ҳ�ͼ�е��ĸ������Σ�ʹ��ÿ�������ε����������
���ڲ������κθ����ߵ�����£����ҳ�ͼ�е��ĸ������Σ�ʹ��ÿ�������ε����������![]() �����
�����![]() ������˵������.
������˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com