
如图6,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=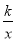 (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )

A.一直增大 B.一直减小
C.先增大后减小 D.先减小后增大
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:2014-2015学年山东省枣庄市九年级4月模拟考试数学试卷(解析版) 题型:选择题
中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )

A.6.75×104吨 B.6.75×103吨 C.6.75×105吨 D.6.75×10﹣4吨
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省德州市九年级下学期第一次练兵考试数学试卷(解析版) 题型:解答题
请同学们认真阅读、研究,完成“类比猜想”及后面的问题.
习题解答:
习题如图(1),点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,说明理由.
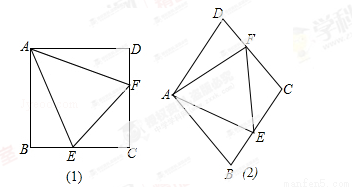
解答:∵正方形ABCD中,AB=AD,∠BAD=∠ADC=∠B=90°,
∴把△ABE绕点A逆时针旋转90°至△ADE′,点F、D、E′在一条直线上.
∴∠E′AF=90°﹣45°=45°=∠EAF,
又∵AE′=AE,AF=AF
∴△AE′F≌△AEF(SAS)
∴EF=E′F=DE′+DF=BE+DF.
习题研究
观察分析:观察图(1),由解答可知,该题有用的条件是①ABCD是四边形,点E、F分别在边BC、CD上;②AB=AD;③∠B=∠D=90°;④∠EAF= ∠BAD.
∠BAD.
类比猜想:(1)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B=∠D时,还有EF=BE+DF吗?
研究一个问题,常从特例入手,请同学们研究:如图13(2),在菱形ABCD中,点E、F分别在BC、CD上,当∠BAD=120°,∠EAF=60°时,还有EF=BE+DF吗?
(2)在四边形ABCD中,点E、F分别在BC、CD上,当AB=AD,∠B+∠D=180°,∠EAF= ∠BAD时,EF=BE+DF吗?
∠BAD时,EF=BE+DF吗?
归纳概括:反思前面的解答,思考每个条件的作用,可以得到一个结论“EF=BE+DF”的一般命题: .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省德州市九年级下学期第一次练兵考试数学试卷(解析版) 题型:填空题
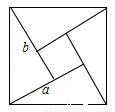
如图,我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形,若小正方形与大正方形的面积之比为1:13,则直角三角形较短的直角边a与较长的直角边b的比值为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省德州市九年级下学期第一次练兵考试数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
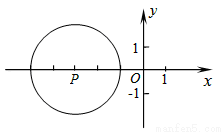
A.1 B.1或5 C.3 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市七年级下学期期中考试数学试卷(解析版) 题型:解答题
(8分)某货主租用汽车运输公司的甲、乙两种货车运货,两次租用的车辆数和运货数如下表所示,问甲、乙两种货车每次能运货多少吨?
第一次 | 第二次 | |
甲种货车车辆数(辆) | 5 | 2 |
乙种货车车辆数(辆) | 3 | 6 |
累计运货数(吨) | 37.5 | 39 |
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市七年级下学期期中考试数学试卷(解析版) 题型:选择题
在下列各式中,运算结果是m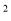 -
- 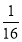 n
n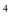 的是( ).
的是( ).
A.(- 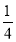 n
n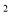 +m)(-
+m)(- 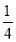 n
n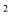 - m)
- m)
B.(m - 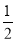 n
n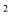 )(m -
)(m - 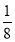 n
n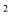 )
)
C.(- 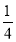 n
n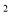 - m)(
- m)(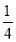 n
n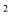 - m)
- m)
D.(- 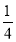 n
n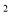 +m)(
+m)(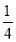 n
n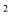 - m)
- m)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com