
如图1,已知A(3,0)、B(4,4)、原点O(0,0)在抛物线y=ax2+bx+c (a≠0)上.

(1)求抛物线的解析式.
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个交点D,求m的值及点D的坐标.
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应)
(1)y=x2-3x
(2)m=4 点D的坐标为(2,-2)
(3)点P的坐标为(- ,-
,- )和(
)和( ,
, )
)
【解析】(1)利用待定系数法求二次函数解析式进而得出答案即可;
(2)首先求出直线OB的解析式为y=x,进而将二次函数以一次函数联立求出交点即可;
(3)首先求出直线A′B的解析式,进而由△P1OD∽△NOB,得出△P1OD∽△N1OB1,进而求出点P1的坐标,再利用翻折变换的性质得出另一点的坐标.
【解析】
(1)∵A(3,0)、B(4,4)、O(0,0)在抛物线y=ax2+bx+c (a≠0)上.
解得:

故抛物线的解析式为:y=x2-3x;
(2)设直线OB的解析式为y=k1x( k1≠0),
由点B(4,4)得
4=4 k1,
解得k1=1.
∴直线OB的解析式为y=x,∠AOB=45°.
∵B(4,4),
∴点B向下平移m个单位长度,
所以平移后的一次函数的解析式为:y=x-m。
又因为平移后的直线与抛物线只有一个交点D,
所以x²-3x=x-m,化简得,x²-4x+m=0,只有一个解,Δ=0.
Δ=4²-4m=0,
故m=4.
∴平移m个单位长度的直线为y=x-4.
解方程组
解得:

∴点D的坐标为(2,-2).
(3)∵直线OB的解析式y=x,且A(3,0).
∵点A关于直线OB的对称点A′的坐标为(0,3).
设直线A′B的解析式为y=k2x+3,此直线过点B(4,4).
∴4k2+3=4,
解得 k2= .
.
∴直线A′B的解析式为y= x+3.
x+3.
∵∠NBO=∠ABO,∴点N在直线A′B上,
设点N(n, n+3),又点N在抛物线y=x2-3x上,
n+3),又点N在抛物线y=x2-3x上,
∴ n+3=n2-3n.
n+3=n2-3n.
解得 n1=- ,n2=4(不合题意,舍去),
,n2=4(不合题意,舍去),
∴点N的坐标为(- ,
, ).
).
如图,将△NOB沿x轴翻折,得到△N1OB1,

则 N1 (- ,-
,- ),B1(4,-4).
),B1(4,-4).
∴O、D、B1都在直线y=-x上.
过D点做DP1∥N1B1,
∵△P1OD∽△NOB,
∴△P1OD∽△N1OB1,
∴P1为O N1的中点.
∴ =
= =
= ,
,
∴点P1的坐标为(- ,-
,- ).
).
将△P1OD沿直线y=-x翻折,可得另一个满足条件的点到x轴距离等于P1到y轴距离,点到y轴距离等于P1到x轴距离,
∴此点坐标为:( ,
, ).
).
综上所述,点P的坐标为(- ,-
,- )和(
)和( ,
, ).
).


科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:选择题
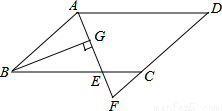
如图,在?ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=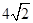 ,则△CEF的面积是( )
,则△CEF的面积是( )
A.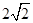 B.
B.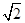 C.
C.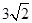 D.
D.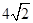
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学二次函数(解析版) 题型:填空题
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
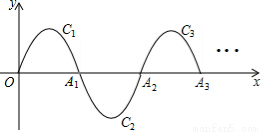
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m=( ).
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学二元一次方程组(解析版) 题型:选择题
为了研究吸烟是否对肺癌有影响,某肿瘤研究所随机地抽查了10000人,并进行统计分析.结果显示:在吸烟者中患肺癌的比例是2.5%,在不吸烟者中患肺癌的比例是0.5%,吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人.如果设这10000人中,吸烟者患肺癌的人数为x,不吸烟者患肺癌的人数为y,根据题意,下面列出的方程组正确的是( )
A.
B.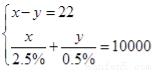
C.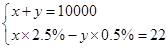
D.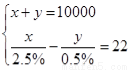
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(二)(解析版) 题型:填空题
如下图,有A、B、C三种型号的卡片,其中A型卡片1张,B型卡片4张,C型卡片5张,现在要从这10张卡片中拿掉一张卡片,余下的全部用上,能拼出(或镶嵌)一个矩形(或正方形),如果图中的小正方格边长均为1cm,则拼出的矩形(或正方形)的面积为 ( )cm2.
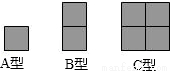
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:选择题
如图,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N.有如下结论:①△ACE≌△DCB,②CM=CN,③AC=DN,④BN=EM.其中正确结论的个数有( )
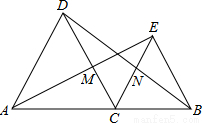
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元一次不等式组(解析版) 题型:填空题
按如下程序进行运算:
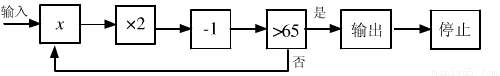
并规定:程序运行到“结果是否大于65”为一次运算,且运算进行4次才停止,则可输入的整数x的个数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com