
如图,△DAC和△EBC都是等边三角形,AE、BD分别与CD、CE交于点M、N.有如下结论:①△ACE≌△DCB,②CM=CN,③AC=DN,④BN=EM.其中正确结论的个数有( )
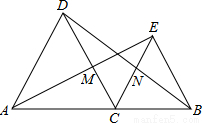
A.1个 B.2个 C.3个 D.4个
C
【解析】本题考查了全等三角形的判定与性质,等边三角形的性质,找出三角形全等的条件,从而证明三角形全等是解题的关键.利用边角边即可证明△ACE与△DCB全等,然后根据全等三角形对应角相等可得∠CAM=∠CDN,再利用角边角证明△ACM与△DCN全等,根据全等三角形对应边相等可得CM=CN,DN=AM,同理可证明△BCN与△ECM全等,根据全等三角形对应边相等可得BN=EM,从而得解.
【解析】
∵△DAC和△EBC都是等边三角形,
∴∠ACD=∠BCE=60°,∴∠ACE=∠DCB=120°,
在△ACE与△DCB中,

∴△ACE≌△DCB(SAS),故①小题正确;
∴∠CAM=∠CDN,
在△ACM与△DCN中,
∴△ACM≌△DCN(ASA),
∴CM=CN,故②小题正确;
DN=AM,
在△AMC中,AC>AM,
∴AC≠DN,故③小题错误;
同理可证:△BCN≌△ECM,
∴BN=EM,故④小题正确.
综上所述,①②④共3个正确.
故选C.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源:2014中考名师推荐数学反比例函数(解析版) 题型:填空题
如图,直线x=2与反比例函数y= 和y=?
和y=? 的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是( ).
的图象分别交于A、B两点,若点P是y轴上任意一点,则△PAB的面积是( ).

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学二次函数综合应用(解析版) 题型:解答题
如图1,已知A(3,0)、B(4,4)、原点O(0,0)在抛物线y=ax2+bx+c (a≠0)上.

(1)求抛物线的解析式.
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个交点D,求m的值及点D的坐标.
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应)
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(二)(解析版) 题型:选择题
小明家装修房屋,用同样的正多边形瓷砖铺地,顶点连着顶点,为铺满地面而不重叠,瓷砖的形状可能有( )
A.正三角形、正方形、正六边形
B.正三角形、正方形、正五边形
C.正方形、正五边形
D.正三角形、正方形、正五边形、正六边形
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:填空题
如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是 ( )
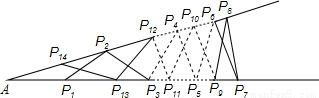
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:选择题
尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于 CD长为半径画弧,两弧交于点P,作射线OP由作法得△OCP≌△ODP的根据是( )
CD长为半径画弧,两弧交于点P,作射线OP由作法得△OCP≌△ODP的根据是( )

A.SAS B.ASA C.AAS D.SSS
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一次函数(解析版) 题型:解答题
2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题:
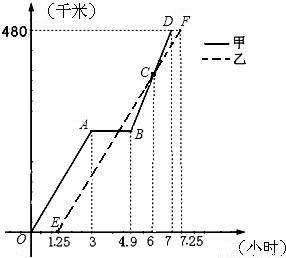
(1)由于汽车发生故障,甲组在途中停留了 小时;
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学一元一次方程(解析版) 题型:选择题
根据流程右边图中的程序,当输出数值y为1时,输入数值x为( )

A.-8 B.8
C.﹣8或8 D.不存在
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省大庆市九年级下学期期末数学试卷(解析版) 题型:选择题
已知x=2是一元二次方程x2+mx+2=0的一个解,则m的值是( )
A.﹣3 B.3 C.0 D.0或3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com