
分析 根据12个队进行单循环赛,每个队都要与除了它自己之外的11个队赛一场,所以一个队的比赛总场数为11.本题中有两个等量关系:胜的场数+平的场数+负的场数=11;胜的积分+平的积分=18.
解答 解:设该队胜x场,平y场,负z场.
则 $\left\{\begin{array}{l}{x+y+z=11}\\{3x+y=18}\end{array}\right.$,
解得 x=$\frac{7+z}{2}$.
若z=1,则x=4,
若z=3,则x=5,
若z=5,则x=6,
所以有三种结果:①x=4,y=6,z=1,②x=5,y=3,z=3,③x=6,y=0,z=5,
所以这个球队可能平0场或3场或6场.
点评 此题主要考查了二元一次方程组的应用,此题中隐含一个等量关系:12个队进行单循环赛,每个队都要与除了它自己之外的11个队赛一场,所以一个队的比赛总场数为11.需要知道这个知识点.


科目:初中数学 来源: 题型:选择题
| A. | (x-$\frac{3}{2}$)2=16 | B. | (2x-$\frac{3}{4}$)2=$\frac{1}{16}$ | C. | (x-$\frac{3}{4}$)2=$\frac{1}{16}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
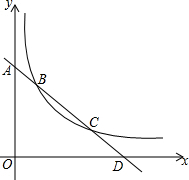 如图,在平面直角坐标系中,直线AD分别交y轴,x轴于A,D两点,与双曲线y=$\frac{k}{x}$(k>0)的一个分支交于点B,C,且满足AB:BC=1:2.
如图,在平面直角坐标系中,直线AD分别交y轴,x轴于A,D两点,与双曲线y=$\frac{k}{x}$(k>0)的一个分支交于点B,C,且满足AB:BC=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
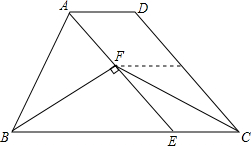 如图,在梯形ABCD中,AD∥BC,AB=CD,AE∥DC交BC于点E,BF⊥AE于F,AD=2,BC=7,CF=4,且∠ABF=∠DCF.
如图,在梯形ABCD中,AD∥BC,AB=CD,AE∥DC交BC于点E,BF⊥AE于F,AD=2,BC=7,CF=4,且∠ABF=∠DCF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6×10-4米 | B. | 6×10-10米 | C. | 6×10-13米 | D. | 6×10-12米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5万名考生是总体 | B. | 800名考生是总体的一个样本 | ||
| C. | 每位考生的数学成绩是个体 | D. | 800名考生是样本容量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com