
【题目】在△ABC中,已知AB=AC,∠BAC=90°,E为边AC上一点,连接BE.
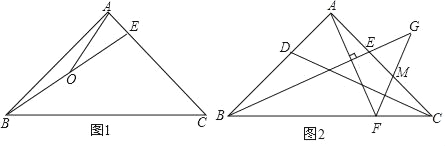
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,D为AB上一点,且满足AE=AD,过点A作AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M,求证:BG=AF+FG.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)如图1中,在AB上取一点M,使得BM=ME,连接ME.,设AE=x,则ME=BM=2x,AM=![]() x,根据AB2+AE2=BE2,可得方程(2x+
x,根据AB2+AE2=BE2,可得方程(2x+![]() x)2+x2=22,解方程即可解决问题.
x)2+x2=22,解方程即可解决问题.
(2)如图2中,作CQ⊥AC,交AF的延长线于Q,首先证明EG=MG,再证明FM=FQ即可解决问题.
解:如图 1 中,在 AB 上取一点 M,使得 BM=ME,连接 ME.
在 Rt△ABE 中,∵OB=OE,
∴BE=2OA=2,
∵MB=ME,
∴∠MBE=∠MEB=15°,
∴∠AME=∠MBE+∠MEB=30°,设 AE=x,则 ME=BM=2x,AM=![]() x,
x,
∵AB2+AE2=BE2,
∴![]() ,
,
∴x=![]() (负根已经舍弃),
(负根已经舍弃),
∴AB=AC=(2+ ![]() )
)![]() ,
,
∴BC= ![]() AB=
AB= ![]() +1.
+1.
作 CQ⊥AC,交 AF 的延长线于 Q,

∵ AD=AE ,AB=AC ,∠BAE=∠CAD,
∴△ABE≌△ACD(SAS),
∴∠ABE=∠ACD,
∵∠BAC=90°,FG⊥CD,
∴∠AEB=∠CMF,
∴∠GEM=∠GME,
∴EG=MG,
∵∠ABE=∠CAQ,AB=AC,∠BAE=∠ACQ=90°,
∴△ABE≌△CAQ(ASA),
∴BE=AQ,∠AEB=∠Q,
∴∠CMF=∠Q,
∵∠MCF=∠QCF=45°,CF=CF,
∴△CMF≌△CQF(AAS),
∴FM=FQ,
∴BE=AQ=AF+FQ=AF=FM,
∵EG=MG,
∴BG=BE+EG=AF+FM+MG=AF+FG.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】已知直线AB上 一点O,以O为端点画射线OC,作∠AOC的角平分线OD,作∠BOC的角平分线OE;

(1)按要求完成画图;
(2)通过观察、测量你发现∠DOE= °;
(3)补全以下证明过程:
证明:∵OD平分∠AOC(已知)
∴∠DOC= ∠AOC( )
∵OE平分∠BOC(已知)
∴∠EOC= ∠BOC( )
∵∠AOC+∠BOC= °
∴∠DOE=∠DOC+∠EOC= (∠AOC+∠BOC)= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1和∠2互补,∠C=∠EDF.
(1)判断DF与EC的关系为 .
(2)试判断DE与BC的关系,并说明理由.
(3)试判断∠DEC与∠DFC的关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天放学后,小红步行,小丽骑自行车沿同一条笔直的马路到图书馆看书,图中线段OA、BC分别表示小红、小丽离开学校的路程s(米)与小红所用的时间t(分钟)的函数关系,根据图象解答下列问题:
(1)小丽比小红迟出发 分钟,小红步行的速度是 米/分钟;(直接写出结果)
(2)两人在路上相距不超过200米的时间有多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
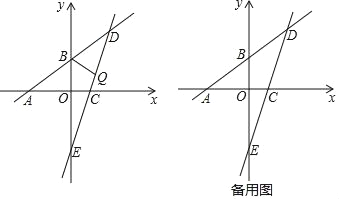
【题目】已知:如图,一次函数![]() 的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
的图象分别与x轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D,点D的横坐标为4,直线CD与y轴相交于点E.
(1)直线CD的函数表达式为 ;(直接写出结果)
(2)点Q为线段DE上的一个动点,连接BQ.
①若直线BQ将△BDE的面积分为1:2两部分,试求点Q的坐标;
②将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上,请直接写出点Q的坐标: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家计划从厂家采购空调和冰箱两种产品共20台,空调的采购单价y1(元/台)与采购数量x1(台)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);冰箱的采购单价y2(元/台)与采购数量x2(台)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经商家与厂家协商,采购空调的数量不少于冰箱数量的 ![]() ,且空调采购单价不低于1200元,问该商家共有几种进货方案?
,且空调采购单价不低于1200元,问该商家共有几种进货方案?
(2)该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱,且全部售完.在(1)的条件下,问采购空调多少台时总利润最大?并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F. 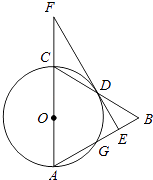
(1)求证:直线EF是⊙O的切线;
(2)若CF=5,cosA= ![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com