
【题目】已知直线AB上 一点O,以O为端点画射线OC,作∠AOC的角平分线OD,作∠BOC的角平分线OE;

(1)按要求完成画图;
(2)通过观察、测量你发现∠DOE= °;
(3)补全以下证明过程:
证明:∵OD平分∠AOC(已知)
∴∠DOC= ∠AOC( )
∵OE平分∠BOC(已知)
∴∠EOC= ∠BOC( )
∵∠AOC+∠BOC= °
∴∠DOE=∠DOC+∠EOC= (∠AOC+∠BOC)= °.
科目:初中数学 来源: 题型:
【题目】试一试,找规律
如图,用火柴棒摆三角形图案,第1个图形需要3根火柴棒,第2个图形需要5根火柴棒……
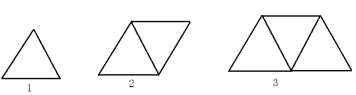
(1)按此规律,第5个图案需要__________根火柴棒.
(2)第n个图案需要___________根火柴棒.
(3)如果用2019根火柴棒去摆,是第____________个图案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=100°
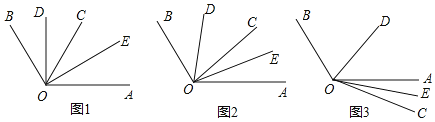
(1)如图1,OC平分∠AOB,OD、OE分别平分∠BOC和∠AOC,求∠DOE的度数;
(2)当OC为∠AOB内任一条射线时,如图2,OD、OE仍是∠BOC和∠AOC的平分线,此时能否求出∠DOE的度数?如果能,请你求出∠DOE的度数;
(3)当OC为∠AOB外任一条射线时,如图3,OD、OE仍是∠BOC和∠AOC的平分线,此时能否求出∠DOE的度数?如果能,请你求出∠DOE的度数;
(4)通过上面几个问题探求,请你用一个结论来表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(2)上题中若∠B=40°,∠C=80°改为∠C>∠B,其他条件不变,请你求出∠EAD与∠B、∠C之间的数列关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )

A. AB=DE B. ∠A=D C. AC=DF D. AC∥DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
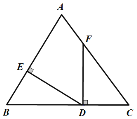
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知AB=AC,∠BAC=90°,E为边AC上一点,连接BE.
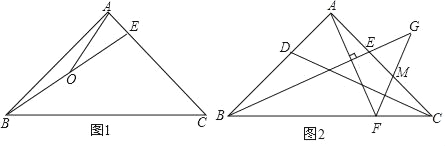
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,D为AB上一点,且满足AE=AD,过点A作AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M,求证:BG=AF+FG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com