
����Ŀ����֪��AOB=100��
��1����ͼ1��OCƽ�֡�AOB��OD��OE�ֱ�ƽ�֡�BOC�͡�AOC�����DOE�Ķ�����
��2����OCΪ��AOB����һ������ʱ����ͼ2��OD��OE���ǡ�BOC�͡�AOC��ƽ���ߣ���ʱ�ܷ������DOE�Ķ���������ܣ����������DOE�Ķ�����
��3����OCΪ��AOB����һ������ʱ����ͼ3��OD��OE���ǡ�BOC�͡�AOC��ƽ���ߣ���ʱ�ܷ������DOE�Ķ���������ܣ����������DOE�Ķ�����
��4��ͨ�����漸������̽��������һ����������ʾ.
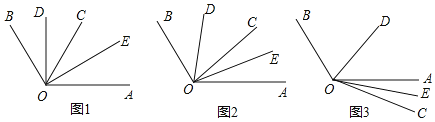
���𰸡���1����DOE=50�㣻��2����DOE=50�㣻��3����DOE=��50�㣻��4������OC�ڡ�AOB���ڲ������ⲿ,���С�DOE=50��.
��������
��1�����ݽ�ƽ���߶��������BOC�͡�AOC���������ɵó��𰸣�
��2�����ݽ�ƽ���߶���ó���COD=![]() ��BOE����COE=
��BOE����COE=![]() ��AOE�������DOE=��COD+��COE=
��AOE�������DOE=��COD+��COE=![]() ��AOB������������ɣ�
��AOB������������ɣ�
��3�����ݽ�ƽ���߶���ó���COD=![]() ��BOE����COE=
��BOE����COE=![]() ��AOE�������DOE=��COD-��COE=
��AOE�������DOE=��COD-��COE=![]() ��AOB������������ɣ�
��AOB������������ɣ�
��4���ɣ�1����2����3���ɵý���.
��1���ߡ�AOB=100�㣬0C�ǡ�AOB��ƽ���ߣ�
���AOB=��BOC=![]() ��AOB=50�㣬
��AOB=50�㣬
��OD��OE�ֱ�ƽ�֡�BOC����AOC��
���COD=![]() ��BOC=25�㣬��COE=
��BOC=25�㣬��COE=![]() ��AOC=25�㣬
��AOC=25�㣬
���DOE=��COD+��COE=25��+25��=50�㣻
��2����OD��OE�ֱ�ƽ�֡�BOC����AOC��
���COD=![]() ��BOE����COE=
��BOE����COE=![]() ��AOE��
��AOE��
���DOE=��COD+��COE=![]() ����BOE+��AOE��=
����BOE+��AOE��=![]() ��AOB=
��AOB=![]() ��100��=50�㣻
��100��=50�㣻
��3���ܣ�
��DOE=��DOC-��COE=![]() ��BOC-
��BOC-![]() ��AOC=
��AOC=![]() ����BOC-��AOC��=
����BOC-��AOC��=![]() ��AOB=
��AOB=![]() ��100��=50�㣮
��100��=50�㣮
��4���ɢ٢ڢۿ�֪:����OC�ڡ�AOB���ڲ������ⲿ,���С�DOE=![]() ��AOB=50��
��AOB=50��


 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ҿ�רӪ����2730Ԫ����A��B�������Ͳ������±���60��,�����ֲ������±��Ľ��ۡ���������ʾ��
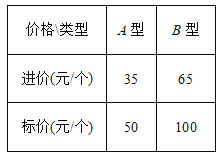
��1�������ֲ������±����������ٸ�?
��2����A�Ͳ������±�����۵�9�۳�����B�Ͳ������±�����۵�8.5�۳��������������������2��A�͡�1��B�Ͳ������±����������ܽ������ۣ����������������±�ȫ���۳������üҾ�רӪ�깲��������Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ��յ���Ҫ�̻���ij�̻���е��˴��������̻��鹤��һ��ʱ�������˹���Ч�ʣ����̻�����ɵ��̻���� S����λ��m2���빤��ʱ�� t����λ��h��֮��ĺ�����ϵ ��ͼ��ʾ������̻�����߹���Ч��ǰÿСʱ��ɵ��̻�����ǣ�������
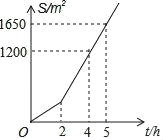
A. 150 m2 B. 300 m2 C. 330 m2 D. 450 m2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A=3x2+3y2��5xy��B=2xy��3y2+4x2��
��1������2B��A��
��2����֪��a|x��2|b2��![]() aby��ͬ�����2B��A��ֵ
aby��ͬ�����2B��A��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ֽ���,С��������һ�š�ABCֽƬ,��D��E�ֱ��DZ�AB��AC��,����ABC����DE�۵�ѹƽ,A��A���غ�,����A=68��,���1+��2=____�㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)(��3pq)2��
(2)��x3��(��4x)2x��
(3)(m4m��m2n)��mn��
(4)(��2)��2��32��(3.144����)0��
(5)(a2)3��(a2)4��(��a2)5��
(6)[��2��3��8��1��(��1)��2]��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��AB�� һ��O����OΪ�˵㻭����OC������AOC�Ľ�ƽ����OD������BOC�Ľ�ƽ����OE��

��1����Ҫ����ɻ�ͼ��
��2��ͨ���۲졢�����㷢�֡�DOE= ��;
��3����ȫ����֤�����̣�
֤������ODƽ�֡�AOC(��֪��
���DOC= ��AOC�� ��
��OEƽ�֡�BOC����֪��
���EOC= ��BOC�� ��
�ߡ�AOC+��BOC= ��
���DOE=��DOC+��EOC= ����AOC+��BOC��= ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BE��ԲO��ֱ����A��EB���ӳ����ϣ�APΪԲO�����ߣ�PΪ�е㣬��PD��ֱ��BE�ڵ�C��
��1����֤����AOD=��APC��
��2����OC��CB=1��2��AB=6����ԲO�İ뾶��tan��APB��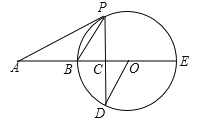
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A����1��5����B����1��0����C����4��3����
(1)�����ABC�������
(2)��ͼ��������ABC����y��ĶԳ�ͼ�Ρ�A1B1C1��
(3)д����A1��B1��C1�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com