
【题目】如图,BE是圆O的直径,A在EB的延长线上,AP为圆O的切线,P为切点,弦PD垂直于BE于点C.
(1)求证:∠AOD=∠APC;
(2)若OC:CB=1:2,AB=6,求圆O的半径及tan∠APB.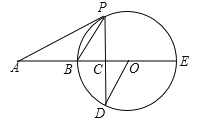
【答案】解:(1)证明:连接OP.
∵OP=OD,∴∠OPD=∠D;
∵PD⊥BE,
∴∠OCD=90°;
在Rt△OCD中,∠D+∠AOD=90°,
又∵AP是⊙O的切线,
∴AP⊥OP,
则∠OPD+∠APC=90°,
∴∠AOD=∠APC;
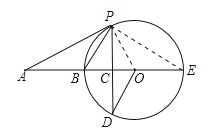
(2)连接PE.
∴∠BPE=90°(直径所对的圆周角是直角);
∵AP是⊙O的切线,
∴∠APB=∠OPE=∠PEA;
∵OC:CB=1:2,
∴设OC=x,则BC=2x,OP=OB=3x;
在Rt△OPC中,OP=3x,OC=x,由勾股定理得:
PC2=OP2﹣OC2=8x2;
在Rt△OPC中,PC⊥OA,由射影定理得:
PC2=OCAC,即8x2=x(2x+6),6x2=6x,
解得x=0(舍去),x=1;
∴OP=OB=3,PC=2![]() ,CE=OC+OE=3+1=4,
,CE=OC+OE=3+1=4,
∴tan∠APB=tan∠PEC=![]() =
=![]() ,
,
∴⊙O的半径为3,∠APB的正切值是![]() .
.
【解析】(1)连接OP.可结合已知的等角和等腰三角形、直角三角形的性质进行证明;
(2)根据OC、BC的比例关系,可用未知数表示出OC、BC的表达式,进而可得OP、OB的表达式;在Rt△AOP中,PC⊥OA,根据射影定理得:PC2=PCAC,PC2的表达式可在Rt△OPC中由勾股定理求得,由此求得未知数的知,从而确定PC、CE的长,也就能求出⊙O的半径和∠APB的正切值.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.
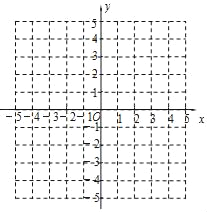
(1)完成下列步骤,画出函数y=|x|的图象;
①列表、填空;
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 1 | 1 | 2 | 3 | … |
②描点;
③连线.
(2)观察图象,当x 时,y随x的增大而增大;
(3)根据图象,不等式|x|<![]() x+
x+![]() 的解集为 .
的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=100°
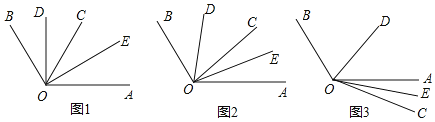
(1)如图1,OC平分∠AOB,OD、OE分别平分∠BOC和∠AOC,求∠DOE的度数;
(2)当OC为∠AOB内任一条射线时,如图2,OD、OE仍是∠BOC和∠AOC的平分线,此时能否求出∠DOE的度数?如果能,请你求出∠DOE的度数;
(3)当OC为∠AOB外任一条射线时,如图3,OD、OE仍是∠BOC和∠AOC的平分线,此时能否求出∠DOE的度数?如果能,请你求出∠DOE的度数;
(4)通过上面几个问题探求,请你用一个结论来表示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE=CF,AB∥DE,添加下列哪个条件不能证明△ABC≌△DEF的是( )

A. AB=DE B. ∠A=D C. AC=DF D. AC∥DF
查看答案和解析>>
科目:初中数学 来源: 题型:
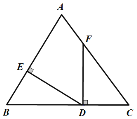
【题目】如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+![]() ∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )
∠C;②AE+BF=EF;③当∠C=90°时,E,F分别是AC,BC的中点;④若OD=a,CE+CF=2b,则S△CEF=ab.其中正确的是( )

A. ①② B. ③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线的夹角为120°,感觉最舒适(如图1),侧面示意图为图2.使用时为了散热,她在底板下垫入散热架ACO′后,电脑转到AO′B′位置(如图3),侧面示意图为图4.已知OA=OB=24cm,O′C⊥OA于点C,O′C=12cm.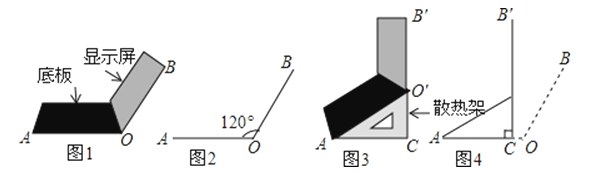
(1)求∠CAO′的度数.
(2)显示屏的顶部B′比原来升高了多少?
(3)如图4,垫入散热架后,要使显示屏O′B与水平线的夹角仍保持120°,则显示屏O′B′应绕点O′按顺时针方向旋转多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O(0,0)、A(2,0)为顶点作正△OAP1 , 以点P1和线段P1A的中点B为顶点作正△P1BP2 , 再以点P2和线段P2B的中点C为顶点作△P2CP3 , …,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是 . 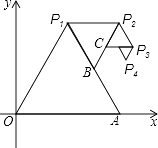
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com