【题目】如图,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别是边AB、AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=68°,则∠1+∠2=____°．
科目：初中数学 来源： 题型：
【题目】定义运算a
b＝a(1－b)，下面给出了关于这种运算的四个结论：
①2(－2)＝6 ②ab＝ba
③若a＋b＝0，则(aa)＋(bb)＝2ab ④若ab＝0，则a＝0．
其中正确结论的序号是 (填上你认为所有正确结论的序号)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“十九大”报告提出了我国将加大治理环境污染的力度，还我青山绿水，其中雾霾天气让环保和健康问题成为焦点，为了调查学生对雾霾天气知识的了解程度，某校在全校学生中抽取400名同学做了一次调查，根据调查统计结果，绘制了不完整的一种统计图表．
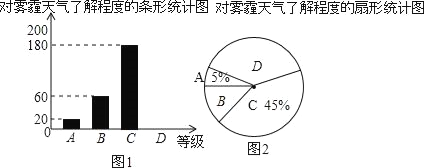
对雾霾了解程度的统计表
对雾霾的了解程度 | 百分比 |
A．非常了解 | 5% |
B．比较了解 | m |
C．基本了解 | 45% |
D．不了解 | n |
请结合统计图表，回答下列问题：
（1）统计表中：m＝ ，n＝ ；
（2）请在图1中补全条形统计图；
（3）请问在图2所示的扇形统计图中，D部分扇形所对应的圆心角是多少度？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学为了解八年级学习体能状况，从八年级学生中随机抽取部分学生进行体能测试，测试结果分为A、B、C、D四个等级．请根据两幅统计图中的信息回答下列问题：
（1）本次抽样调查共抽取了多少名学生？
（2）求测试结果为C等级的学生数，并补全条形图；
（3）若该中学八年级共有700名学生，请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名．
查看答案和解析>>
科目：初中数学 来源： 题型：
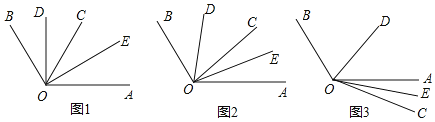
【题目】已知∠AOB=100°
（1）如图1，OC平分∠AOB，OD、OE分别平分∠BOC和∠AOC，求∠DOE的度数；
（2）当OC为∠AOB内任一条射线时，如图2，OD、OE仍是∠BOC和∠AOC的平分线，此时能否求出∠DOE的度数？如果能，请你求出∠DOE的度数；
（3）当OC为∠AOB外任一条射线时，如图3，OD、OE仍是∠BOC和∠AOC的平分线，此时能否求出∠DOE的度数？如果能，请你求出∠DOE的度数；
（4）通过上面几个问题探求，请你用一个结论来表示.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图，在△ABC中，∠B=40°，∠C=80°，AD⊥BC于D，且AE平分∠BAC，求∠EAD的度数．
（2）上题中若∠B=40°，∠C=80°改为∠C＞∠B，其他条件不变，请你求出∠EAD与∠B、∠C之间的数列关系？并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D，下列四个结论：
①∠AOB=90°+
∠C；②AE+BF=EF；③当∠C=90°时，E，F分别是AC，BC的中点；④若OD=a，CE+CF=2b，则S△CEF=ab．其中正确的是（ ）
A. ①② B. ③④ C. ①②④ D. ①③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知：∠MON=30°，点A1、A2、A3在射线ON上，点B1、B2、B3…在射线OM上，△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形，若OA1=1，则△A6B6A7的边长为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
