
【题目】计算下列各题
(1)化简:( ![]() ﹣1)÷
﹣1)÷ ![]()
(2)关于x的一元二次方程kx2+2x﹣3=0有两个不相等的实数根,求k的取值范围.
【答案】
(1)解:原式=( ![]() ﹣
﹣ ![]() )
) ![]()
=﹣ ![]()
![]()
=﹣ ![]()
(2)解:∵关于x的一元二次方程kx2+2x﹣3=0有两个不相等的实数根,
∴k≠0,且△>0,即22﹣4×k×(﹣3)>0,
解得k>﹣ ![]() 且k≠0
且k≠0
【解析】(1)先将括号内的式子通分,再将除法转化为乘法,然后约分计算即可;(2)根据一元二次方程的定义以及根的判别式得到k≠0且△>0,即22﹣4×k×(﹣3)>0,然后解两个不等式即可得到k的取值范围.
【考点精析】解答此题的关键在于理解分式的混合运算的相关知识,掌握运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]},以及对求根公式的理解,了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




查看答案和解析>>
科目:初中数学 来源: 题型:
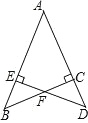
【题目】如图,△ABC,△ADE 均是等腰直角三角形,BC 与 DE 相交于 F 点,若 AC=AE=1,则四边形 AEFC 的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
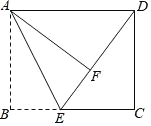
【题目】如图,在长方形 ABCD 中,AB=8,AD=10,点 E 为 BC 上一点,将△ABE 沿 AE 折叠,使点 B 落在长方形内点 F 处, 且 DF=6,求 BE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
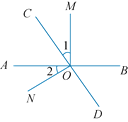
【题目】如图,直线AB,CD相交于点O,过点O作两条射线OM,ON,且∠AOM=∠CON=90°.
(1)若OC平分∠AOM,求∠AOD的度数;
(2)若∠1=∠BOC,求∠AOC和∠MOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一长方形花园用来种植菊花和郁金香,其余作为休息区;
(1)求种植菊花和郁金香的面积;
(2)当![]() m,
m,![]() m时,种植菊花和郁金香的面积是多少m2?
m时,种植菊花和郁金香的面积是多少m2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com