
【题目】四边形ABCD中,BD是对角线,∠ABC=90 °,tan∠ABD= ![]() ,AB=20,BC=10,AD=13,则线段CD=________.
,AB=20,BC=10,AD=13,则线段CD=________.
【答案】17或![]() .
.
【解析】
作AH⊥BD于H,CG⊥BD于G,根据正切的定义分别求出AH、BH,根据勾股定理求出HD,得到BD,根据勾股定理计算即可.
当∠ADB为锐角时,作AH⊥BD于H,CG⊥BD于G,
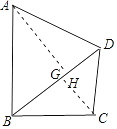
∵tan∠ABD=![]() ,
,
∴ ![]() =
=![]() ,
,
设AH=3x,则BH=4x,
由勾股定理得,(3x)2+(4x)2=202,
解得,x=4,
则AH=12,BH=16,
在Rt△AHD中,HD=![]() =5,
=5,
∴BD=BH+HD=21,
∵∠ABD+∠CBD=90°,∠BCH+∠CBD=90°,
∴∠ABD=∠CBH,
∴ ![]() =
=![]() ,又BC=10,
,又BC=10,
∴BG=6,CG=8,
∴DG=BD﹣BG=15,
∴CD=![]() =17,
=17,
当∠ADB为钝角时,CD′=![]() =
=![]() ,
,
故答案为:17或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
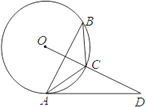
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
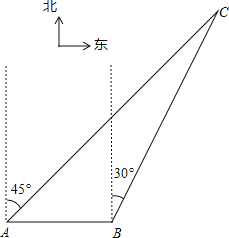
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣2,0),B(0,![]() ),C(4,0),其对称轴与x轴交于点D,若P为y轴上的一个动点,连接PD,
),C(4,0),其对称轴与x轴交于点D,若P为y轴上的一个动点,连接PD,![]() PB+PD的最小值为________.
PB+PD的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
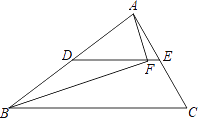
A.如图,DE为△ABC的中位线,点F为DE上一点,且∠AFB=90°,若AB=8,BC=10,则EF的长为________.
B.小智同学在距大雁塔塔底水平距离为138米处,看塔顶的仰角为24.8(不考虑身高因素),则大雁塔市约为________米.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机销售商从厂家购进了![]() 两种型号的手机,已知一台
两种型号的手机,已知一台![]() 型手机的进价比一台
型手机的进价比一台![]() 型手机的进价多300元,用7500元购进
型手机的进价多300元,用7500元购进![]() 型手机和用6000元购进
型手机和用6000元购进![]() 型手机的数量相同.
型手机的数量相同.
(1)求一台![]() 型手机和一台
型手机和一台![]() 型手机的进价各是多少元?
型手机的进价各是多少元?
(2)在销售过程中,![]() 型手机因为性价比高,更受消费者的欢迎.为了增大
型手机因为性价比高,更受消费者的欢迎.为了增大![]() 型手机的销量,该销售商决定对
型手机的销量,该销售商决定对![]() 型手机进行降价销售.经调查,当
型手机进行降价销售.经调查,当![]() 型手机的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台.如果每天销售
型手机的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台.如果每天销售![]() 型手机的利润为3200元,请问该手机销售商应将
型手机的利润为3200元,请问该手机销售商应将![]() 型手机的售价降低多少元?
型手机的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
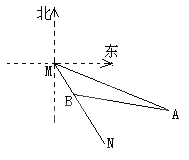
【题目】如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心.以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m.通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?(![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
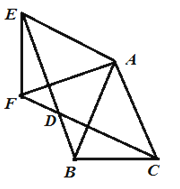
【题目】如图△ABC,AB=AC,将△ABC绕点A顺时针旋转得到△AEF,连结BE、CF相交于点D.
(1)求证:BE=CF;
(2)已知四边形ACDE是菱形,∠BAC=45°,AB=AC=1.
①求旋转角 ∠BAE的度数;
②求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com