
【题目】如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
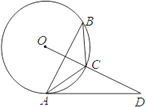
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知直线![]() (其中
(其中![]() 为常数,
为常数,![]() ),
),![]() 取不同数值时,可得不同直线,请研究这些直线的共同特征.
取不同数值时,可得不同直线,请研究这些直线的共同特征.
实践操作
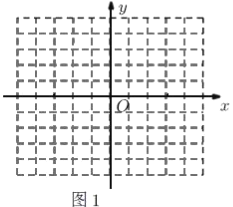
(1)当![]() 时,直线
时,直线![]() 的解析式为________,请在图1中画出图象.
的解析式为________,请在图1中画出图象.
当![]() 时,直线
时,直线![]() 的解析式为________,请在图2中画出图象
的解析式为________,请在图2中画出图象
(2)探索发现:
直线![]() 必经过点(_______,_______).
必经过点(_______,_______).
(3)类比迁移:
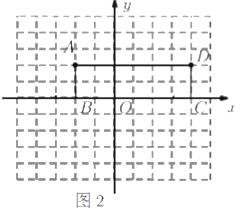
矩形![]() 如图2所示,若直线
如图2所示,若直线![]() 分矩形
分矩形![]() 的面积为相等的两部分,请在图中直接画出这条直线.
的面积为相等的两部分,请在图中直接画出这条直线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有3个带号码的球,球号分别为2,3,4,这些球除号码不同外其它均相同。甲、乙、两同学玩摸球游戏,游戏规则如下:
先由甲同学从中随机摸出一球,记下球号,并放回搅匀,再由乙同学从中随机摸出一球,记下球号。将甲同学摸出的球号作为一个两位数的十位上的数,乙同学的作为个位上的数。若该两位数能被4整除,则甲胜,否则乙胜.
问:这个游戏公平吗?请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC与点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.下列结论:①CD2=CE·CB;②4EF 2=ED ·EA;③∠OCB=∠EAB;④![]() .其中正确的只有____________________.(填序号)
.其中正确的只有____________________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
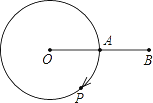
【题目】如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s);
(1)当t=6s时,∠POA的度数是________;
(2)当t为多少时,∠POA=120°;
(3)如果点B是OA延长线上的一点,且AB=AO,问t为多少时,△POB为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
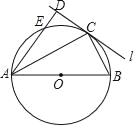
【题目】如图,AB为⊙O的直径,直线l经过⊙O上一点C,过点A作AD⊥l于点D,交⊙O于点E,AC平分∠DAB.
(1)求证:直线l是⊙O的切线;
(2)若DC=4,DE=2,求线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a 的值
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b),
展开,得2x2+x+a =2x2+(b+4)x+2b,
所以![]() ,解得
,解得![]() ,
,
所以,另一个因式是(2x3),a 的值是6.
请你仿照以上做法解答下题:已知二次三项式3x2 10x m 有一个因式是(x+4),求另一个因式以及m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com