
【题目】如图,AB为⊙O的直径,直线l经过⊙O上一点C,过点A作AD⊥l于点D,交⊙O于点E,AC平分∠DAB.
(1)求证:直线l是⊙O的切线;
(2)若DC=4,DE=2,求线段AB的长.
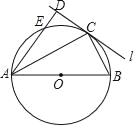
【答案】(1)详见解析;(2)AB=10.
【解析】
(1)连接OC,由OA=OC可以得到∠OAC=∠OCA,然后利用角平分线的性质可以证明∠DAC=∠OCA;随之利用垂直即可解答.
(2) 连接BE交CO于M,得出四边形DEMC是矩形,利用勾股定理即可解答.
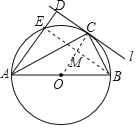
(1)证明:连接OC,
∵AC平分∠DAB,
∴∠DAC=∠OAC,
又∵OA=OC,
∴∠OCA=∠OAC,
∴∠DAC=∠OCA,
又∵CD⊥AD,即∠ADC=90°,
∴∠DAC+∠DCA=90°,
∴∠OCA+∠DCA=90°,即∠OCD=90°,
∴OC⊥CD,
则CD是圆O的切线;
(2)解:连接BE交CO于M,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴四边形DEMC是矩形,
∴OC⊥BE,
∴BM=EM=CD=4,
在Rt△OMB中,BM2+OM2=OB2,
∴42+(r﹣2)2=r2,
∴r=5,
∴AB=10.


科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°,AB=![]() BC=1,则下列结论:
BC=1,则下列结论:
①∠CAD=30°②BD=![]() ③S平行四边形ABCD=ABAC④OE=
③S平行四边形ABCD=ABAC④OE=![]() AD⑤S△APO=
AD⑤S△APO=![]() ,正确的个数是( )
,正确的个数是( )
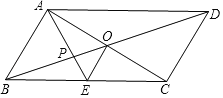
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
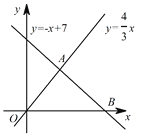
【题目】如图,已知一次函数![]() 与正比例函数
与正比例函数![]() 的图象交于点
的图象交于点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() .
.
(1)直接写出点![]() 的坐标为 ;点
的坐标为 ;点![]() 的坐标为 ;
的坐标为 ;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线l∥y轴.动点
作直线l∥y轴.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长的速度,沿
个单位长的速度,沿![]() 的路线向点
的路线向点![]() 运动;同时直线
运动;同时直线![]() 从点
从点![]() 出发,以相同速度向左平移,在平移过程中,直线
出发,以相同速度向左平移,在平移过程中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 或线段
或线段![]() 于点
于点![]() .当点
.当点![]() 到达点
到达点![]() 时,点
时,点![]() 和直线
和直线![]() 都停止运动.在运动过程中,设动点
都停止运动.在运动过程中,设动点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
![]() 当
当![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形的面积为
为顶点的三角形的面积为![]() ;
;
![]() 是否存在以
是否存在以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形?若存在,直接写出
为顶点的三角形是等腰三角形?若存在,直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
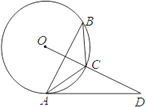
(1)AD是⊙O的切线吗?为什么?
(2)若OD⊥AB,BC=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “打开电视机,正在播《动物世界》”是随机事件
B. 某种彩票的中奖概率为千分之一,说明每买1000张彩票,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为三分之一
D. 任意画一个三角形,其内角和为360°是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
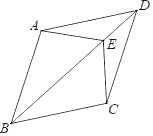
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果∠BDC=30°,DE=2,EC=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的图像如图所示,那么关于x的方程ax2+bx+c-4=0的根的情况是( )

A.有两个不相等的实数根 B.有两个异号的实数根
C.有两个相等的实数根 D.没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
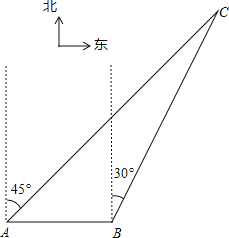
【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
查看答案和解析>>
科目:初中数学 来源: 题型:
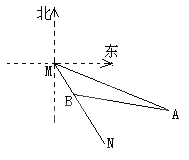
【题目】如图所示,MN表示某饮水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°的方向上有一点A,以点A为圆心.以500m为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为南偏东75°,已知MB=400m.通过计算回答,如果不改变方向,输水路线是否会穿过该居民区?(![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com