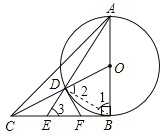
【题目】已知：如图，AB=BC，∠ABC=90°，以AB为直径的⊙O交OC与点D，AD的延长线交BC于点E，过D作⊙O的切线交BC于点F．下列结论：①CD2=CE·CB；②4EF 2=ED ·EA；③∠OCB=∠EAB；④．其中正确的只有____________________．（填序号）

参考答案：

【答案】①、②、④

【解析】试题分析：先连接BD，利用相似三角形的判定以及切线的性质定理得出DF=FB，进而分别得出△CDE∽△CBD以及△CDF∽△CBO，再根据相似三角形的性质分别分析即可得出答案.

①连接BD，∵AB为直径，∴∠ADB=90°，∴∠DBE+∠3=90°，∵∠ABC=90°，

∴∠1+∠DBE=90°，∴∠1=∠3，又∵DO=BO，∴∠1=∠2，∴∠2=∠3，

∴∠CDB=∠CED，∵∠DCB=∠ECD，∴△CDE∽△CBD，∴，故①正确；

②∵过D作⊙O的切线交BC于点F，∴FD是⊙O的切线，∵∠ABC=90°，

∴CB是⊙O的切线，∴FB=DF，∴∠FDB=∠FBD，∴∠1=∠FDE，∴∠FDE=∠3，

∴DF=EF，∴EF=FB，∴EB=2EF，∵在Rt△ABE中，BD⊥AE，∴，

∴，故②正确；

③∵AO=DO，∴∠OAD=∠ADO，假设③∠OCB=∠EAB成立，则∠OCB=0.5∠COB，

∴∠OCB=30°，而 ，与tan30°= 矛盾，

故③∠OCB=∠EAB不成立，故此选项错误；

④∵∠CDF=∠CBO=90°，∠DCF=∠OCB，∴△CDF∽△CBO，∴ ，∴ ，

∵AB=BC，∴DF=0.5CD；故④正确．

关闭