Question

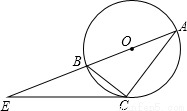
如图，已知AB为⊙O的直径，E是AB延长线上一点，点C是⊙O上的一点，连结EC、BC、AC，且∠BCE＝∠BAC.

（1）求证：EC是⊙O的切线.

（2）过点A作AD垂直于直线EC于D，若AD＝3，DE＝4，求⊙O的半径.

 

 

Answer 1

（1）证明见解析；（2）.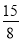

【解析】

试题分析：（1）连结OC，根据圆周角定理由AB是⊙O的直径得∠1+∠2=90°，而∠1=∠A，∠A=∠BCE，所以∠BCE=∠1，即∠BCE+∠2=90°，然后根据切线的判定定理即可得到EC是⊙O的切线.

（2）设⊙O的半径为r，在Rt△ADE中利用勾股定理计算出AE=5，则OE=5-r，OC=r，咋证明△EOC∽△EAD，利用相似比得到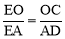 ，即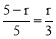，然后解方程即可得到圆的半径．

（1）如图，连接OC，

∵AB是⊙O的直径，∴∠ACB＝90°，即∠1＋∠2＝90°.

∵OC＝OA，∴∠1＝∠A.

又∵∠A＝∠BCE，∴∠BCE＝∠1.

∴∠BCE＋∠2＝90°，即OC⊥EC.

又EC过半径OC的外端，∴EC是⊙O的切线.

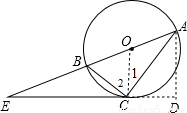
（2）由（1）可知OC⊥EC，

又AD⊥EC，∴OC∥AD. ∴△EOC∽△EAD. ∴.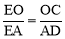

设⊙O的半径为r,

在Rt△ADE中AD＝3，ED＝4，则AE＝5,

∴OE＝5－r；OC＝r.

∴.

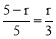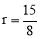∴, 即⊙O的半径为.

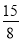考点：1.切线的判定；2.相似三角形的判定与性质．