
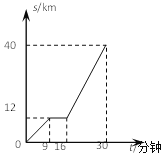
【题目】如图是某汽车行驶的路程s(km)与时间t(分钟) 的函数关系图。观察图中所提供的信息,解答下列问题:
(1)求汽车在前9分钟内的平均速度.
(2)汽车在中途停留的时间.
(3)求该汽车行驶30千米的时间.
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点,△PAB,△PMN都是等边三角形,连接BN,

(1)求证:AM=BN;
(2)写出点M在如图2所示位置时,线段AB、BM、BN三者之间的数量关系,并给出证明;
(3)点M在图3所示位置时,直接写出线段AB、BM、BN三者之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣8)﹣(﹣15)+(﹣9)﹣(﹣12)
(2)7![]() +(﹣6.5)+3
+(﹣6.5)+3![]() +(﹣1.25)+2
+(﹣1.25)+2![]()
(3)(﹣81)÷(﹣2![]() )×
)×![]() ÷(﹣8)
÷(﹣8)
(4)![]()
(5)![]()
(6)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
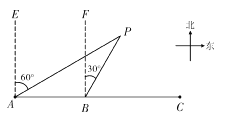
【题目】如图所示,C城市在A城市正东方向,现计划在A,C两城市间修建一条高速铁路(即线段AC),经测量,森林保护区的中心P在城市A的北偏东60°方向上,在线段AC上距A城市120 km的B处测得P在北偏东30°方向上,已知森林保护区是以点P为圆心,100 km为半径的圆形区域,请问计划修建的这条高速铁路是否穿越保护区,为什么?(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于0.000 002 5 m的颗粒物,将0.000 002 5用科学记数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张和同学相约“五一”节到离家2400米的电影院看电影,到电影院后,发现电影票忘带了,此时离电影开始还有25分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回电影院,已知小张骑车的时间比跑步的时间少用了4分钟,骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了6分钟,他能否在电影开始前赶到电影院?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中学习中,我们知道:点到直线的距离是直线外一点和直线上各点连接的所有线段中,最短的线段(即垂线段)的长度.类比,我们给出点到某一个图形的距离的定义:点P与图形l上各点连接的所有线段中,若线段PA1最短,则线段PA1的长度称为点P到图形l的距离,记为d(P,图形l).特别地,点P在图形上,则点P到图形的距离为0,即d(P,图形)=0.
(1)若点P是⊙O内一点,⊙O的半径是5,OP=2,则d(P,⊙O)= .
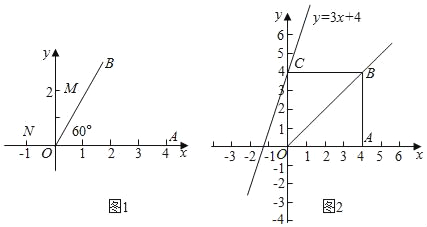
(2)如图1,在平面直角坐标系xOy中,A(4,0).若M(0,2),N(﹣1,0),则d(M,∠AOB)= ,d(N,∠AOB)= .
(3)在正方形OABC中,点B(4,4),如图2,若点P在直线y=3x+4上,且d(P,∠AOB)=2![]() ,求点P的坐标;
,求点P的坐标;
(4)已知点P(m+1,2m﹣3),以点E(1,0)为圆心,EO长为半径作⊙E,则d(P,⊙E)的最小值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com