
【题目】计算下列各题
(1)1+(﹣2)+|﹣2﹣3|﹣5
(2)﹣24﹣ ![]() ×[5﹣(﹣3)2]
×[5﹣(﹣3)2]
(3)( ![]() +1
+1 ![]() ﹣2.75)×(﹣24)+(﹣12016).
﹣2.75)×(﹣24)+(﹣12016).
(4)[50﹣( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣6)2]÷(﹣7)2 .
)×(﹣6)2]÷(﹣7)2 .
【答案】
(1)解:1+(﹣2)+|﹣2﹣3|﹣5
=1﹣2+5﹣5
=﹣1;
(2)解:﹣24﹣ ![]() ×[5﹣(﹣3)2]
×[5﹣(﹣3)2]
=﹣16﹣ ![]() ×[5﹣9]
×[5﹣9]
=﹣16﹣ ![]() ×[﹣4]
×[﹣4]
=﹣16+2
=﹣14
(3)解:( ![]() +1
+1 ![]() ﹣2.75)×(﹣24)+(﹣12016).
﹣2.75)×(﹣24)+(﹣12016).
=﹣ ![]() ×24﹣1
×24﹣1 ![]() ×24+2.75×24﹣1
×24+2.75×24﹣1
=﹣3﹣32+66﹣1
=﹣36+66
=30;
(4)解:[50﹣( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣6)2]÷(﹣7)2
)×(﹣6)2]÷(﹣7)2
=[50﹣( ![]() ﹣
﹣ ![]() +
+ ![]() )×36]÷49
)×36]÷49
=[50﹣ ![]() ×36+
×36+ ![]() ×36﹣
×36﹣ ![]() ×36]÷49
×36]÷49
=(50﹣28+33﹣6)÷49
=49÷49
=1.
【解析】(1)先算绝对值,再算加减法;(2)(3)(4)先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.
【考点精析】根据题目的已知条件,利用有理数的四则混合运算的相关知识可以得到问题的答案,需要掌握在没有括号的不同级运算中,先算乘方再算乘除,最后算加减.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,C是AB的中点,且a、b满足|a+3|+(b+3a)2=0. ![]()
(1)求点C表示的数;
(2)点P从A点以3个单位每秒向右运动,点Q同时从B点以2个单位每秒向左运动,若AP+BQ=2PQ,求时间t;
(3)若点P从A向右运动,点M为AP中点,在P点到达点B之前:① ![]() 的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
的值不变;②2BM﹣BP的值不变,其中只有一个正确,请你找出正确的结论并求出其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形的三边a,b,c能满足a2+b2=nc2(n为正整数),那么这个三角形叫做“n阶三角形”.如三边分别为1、2、![]() 的三角形满足12+22=1×(
的三角形满足12+22=1×(![]() )2,所以它是1阶三角形,但同时也满足(
)2,所以它是1阶三角形,但同时也满足(![]() )2+22=9×12,所以它也是9阶三角形.显然,等边三角形是2阶三角形,但2阶三角形不一定是等边三角形.
)2+22=9×12,所以它也是9阶三角形.显然,等边三角形是2阶三角形,但2阶三角形不一定是等边三角形.
(1)在我们熟知的三角形中,何种三角形一定是3阶三角形?
(2)若三边分别是a,b,c(a<b<c)的直角三角形是一个2阶三角形,求a:b:c.
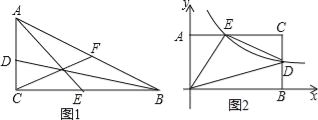
(3)如图1,直角△ABC是2阶三角形,AC<BC<AB,三条中线BD、AE、CF所构成的三角形是何种三角形?四位同学作了猜想:
A同学:是2阶三角形但不是直角三角形;
B同学:是直角三角形但不是2阶三角形;
C同学:既是2阶三角形又是直角三角形;
D同学:既不是2阶三角形也不是直角三角形.
请你判断哪位同学猜想正确,并证明你的判断.
(4)如图2,矩形OACB中,O为坐标原点,A在y轴上,B在x轴上,C点坐标是(2,1),反比例函数y=![]() (k>0)的图象与直线AC、直线BC交于点E、D,若△ODE是5阶三角形,直接写出所有可能的k的值.
(k>0)的图象与直线AC、直线BC交于点E、D,若△ODE是5阶三角形,直接写出所有可能的k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了调查学生备战中考体育的训练情况,特抽查了40名学生进行了模拟测试(满分70分),体育组根据抽测成绩制成如表格:
抽测成绩/cm | 50 | 54 | 59 | 62 | 67 | 70 |
人数 | 2 | 7 | 6 | 6 | 15 | 4 |
则这批考生模拟成绩的中位数和众数分别是( )
A. 59,59B. 59,62C. 62,67D. 62,62
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )

A. 甲的速度随时间的增加而增大
B. 乙的平均速度比甲的平均速度大
C. 在起跑后第180秒时,两人相遇
D. 在起跑后第50秒时,乙在甲的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
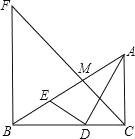
【题目】如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论①∠AED=∠ADC;②![]() ;③ACBE=12;④3BF=4AC,其中结论正确的个数有( )
;③ACBE=12;④3BF=4AC,其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
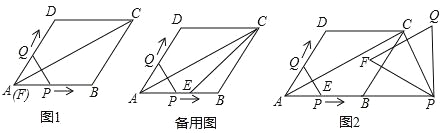
【题目】已知:如图1,菱形ABCD的边长为6,∠DAB=60°,点E是AB的中点,连接AC、EC.点Q从点A出发,沿折线A﹣D﹣C运动,同时点P从点A出发,沿射线AB运动,P、Q的速度均为每秒1个单位长度;以PQ为边在PQ的左侧作等边△PQF,△PQF与△AEC重叠部分的面积为S,当点Q运动到点C时P、Q同时停止运动,设运动的时间为t.
(1)当等边△PQF的边PQ恰好经过点D时,求运动时间t的值;当等边△PQF的边QF 恰好经过点E时,求运动时间t的值;
(2)在整个运动过程中,请求出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,当点Q到达C点时,将等边△PQF绕点P旋转α°(0<α<360),直线PF分别与直线AC、直线CD交于点M、N.是否存在这样的α,使△CMN为等腰三角形?若存在,请直接写出此时线段CM的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com