
【题目】如图,Rt△ABC中,AC⊥BC,AD平分∠BAC交BC于点D,DE⊥AD交AB于点E,M为AE的中点,BF⊥BC交CM的延长线于点F,BD=4,CD=3.下列结论①∠AED=∠ADC;②![]() ;③ACBE=12;④3BF=4AC,其中结论正确的个数有( )
;③ACBE=12;④3BF=4AC,其中结论正确的个数有( )
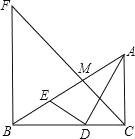
A.1个 B.2个 C.3个 D.4个
【答案】C.
【解析】
试题分析:①∠AED=90°﹣∠EAD,∠ADC=90°﹣∠DAC,∵∠EAD=∠DAC,
∴∠AED=∠ADC.故本选项正确;
②∵AD平分∠BAC,∴![]() ,∴设AB=4x,则AC=3x,
,∴设AB=4x,则AC=3x,
在直角△ABC中,AC2+BC2=AB2,则(3x)2+49=(4x)2,
解得:x=![]() ,
,
∵∠EAD=∠DAC,∠ADE=∠ACD=90°,
∴△ADE∽△ACD,得DE:DA=DC:AC=3:![]() ,故不正确;
,故不正确;
③由①知∠AED=∠ADC,
∴∠BED=∠BDA,
又∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴DE:DA=BE:BD,由②知DE:DA=DC:AC,
∴BE:BD=DC:AC,
∴ACBE=BDDC=12.
故本选项正确;
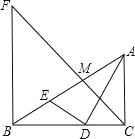
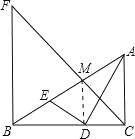
④连接DM,
在Rt△ADE中,MD为斜边AE的中线,
则DM=MA.
∴∠MDA=∠MAD=∠DAC,
∴DM∥BF∥AC,
由DM∥BF得FM:MC=BD:DC=4:3;
由BF∥AC得△FMB∽△CMA,有BF:AC=FM:MC=4:3,
∴3BF=4AC.
故本选项正确.
综上所述,①③④正确,共有3个.
故选C.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】计算题计算:
(1)(﹣ ![]() ﹣
﹣ ![]() +
+ ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣60)
)×(﹣60)
(2)﹣23﹣(1﹣0.5)× ![]() ×[2﹣(﹣3)2]
×[2﹣(﹣3)2]
(3)(4x2y﹣3xy2)﹣(1+4x2y﹣3xy2)
(4)5(a2b﹣2ab2+c)﹣4(2c+3a2b﹣ab2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)1+(﹣2)+|﹣2﹣3|﹣5
(2)﹣24﹣ ![]() ×[5﹣(﹣3)2]
×[5﹣(﹣3)2]
(3)( ![]() +1
+1 ![]() ﹣2.75)×(﹣24)+(﹣12016).
﹣2.75)×(﹣24)+(﹣12016).
(4)[50﹣( ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣6)2]÷(﹣7)2 .
)×(﹣6)2]÷(﹣7)2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
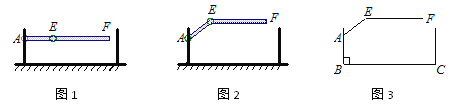
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com