
【题目】一次函数y=(k-![]() )x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
)x-3k+10(k为偶数)的图象经过第一、二、三象限,与x轴、y轴分别交于A、B两点,过点B作一直线与坐标轴围成的三角形面积为2,交x轴于点C.
(1)求该一次函数的解析式;
(2)若一开口向上的抛物线经过点A、B、C三点,求此抛物线的解析式。
(3)过(2)中的A、B、C三点作△ABC,求tan∠ABC的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)求该一次函数y=(k-![]() )x-3k+10(k为偶数)的解析式,需求出k的值,根据图象经过第一、二、三象限,得到k的取值范围,确定k的值,得到一次函数的解析式为y=
)x-3k+10(k为偶数)的解析式,需求出k的值,根据图象经过第一、二、三象限,得到k的取值范围,确定k的值,得到一次函数的解析式为y=![]() x+4.
x+4.
(2)求抛物线的解析式,可用待定系数法,需要求出A,B,C三点的坐标,
先根据一次函数的解析式求出A、B两点的坐标,再由S△BOC=2,求出C点坐标.
(3)要求tan∠ABC的值,根据正切函数的定义,构造一个以∠ABC为内角的直角三角形,过C作CD⊥AB于D,则tan∠ABC=![]() .由于已知A、B、C三点的坐标,可根据三角函数的定义分别求出DC,AD的值,再算出BD的值.
.由于已知A、B、C三点的坐标,可根据三角函数的定义分别求出DC,AD的值,再算出BD的值.
试题解析:⑴(4分)由题意得: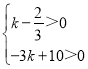 ,解得
,解得![]() ,又k为偶数
,又k为偶数
∴k=2∴一次函数的解析式为![]()
⑵(4分)求得A(-3,0)、B(0,4),∴OB=4
∵![]() =2OC=2,∴OC=1
=2OC=2,∴OC=1
∴C(1,0)或(-1,0)
若取C(1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x-1),
将B(0,4)代入,求得![]() ,舍.
,舍.
若取C(-1,0)、A(-3,0)、B(0,4),设y=a(x+3)(x+1),
将B(0,4)代入,求得![]() ,
,
∴抛物线为![]()
⑶(4分)如图,过C作CD⊥AB于D,则tan∠ABC=![]()
∵ Sin∠BAO=![]() ,cos∠BAO=
,cos∠BAO=![]()
∴ ![]() , DC=
, DC=![]() ,
,![]() ,AD=
,AD=![]() ,∴BD=
,∴BD=![]()
∴ tan∠ABC=![]() (用相似证明也对)
(用相似证明也对)



科目:初中数学 来源: 题型:
【题目】(18分)计算与化简:
⑴ -3-(-9)+5
⑵ (1-![]() +
+![]() )×(-48)
)×(-48)
⑶16÷(-2)3-(-![]() )×(-4)
)×(-4)
⑷-12-(-10)÷![]() ×2+(-4)2
×2+(-4)2
⑸ -23-(2-1.5)÷![]() ×∣-6-(-3)2∣
×∣-6-(-3)2∣
⑹-9a2+[2a2-2(a-3a2)+5a]
查看答案和解析>>
科目:初中数学 来源: 题型:
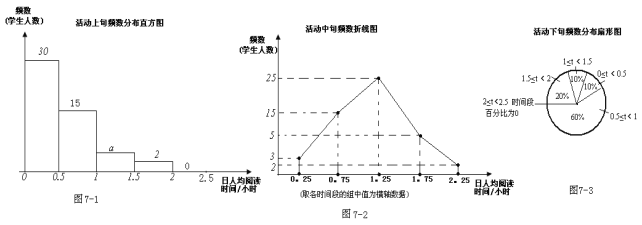
【题目】以下统计图描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、下旬)日人均阅读时间的情况:
(1)从以上统计图可知,九年级(1)班共有学生 人;
(2)图7-1中a的值是 ;
(3)从图7-1、7-2中判断,在这次读书月活动中,该班学生每日阅读时间 (填“普遍增加了”或“普遍减少了”);
(4)通过这次读书月活动,如果该班学生初步形成了良好的每日阅读习惯,参照以上统计图的变化趋势,至读书月活动结束时,该班学生日人均阅读时间在0.5~1小时的人数比活动开展初期增加了 人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,4秒后,两点相距16个单位长度.已知点B的速度是点A的速度的3倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动4秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,再过几秒时,原点恰好处在AB的中点?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从原点O位置出发向B点运动,且C的速度是点A的速度的一半;当点C运动几秒时,C为AB的中点?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=2x2+4x﹣5,设自变量的值分别为x1、x2、x3 , 且﹣1<x1<x2<x3 , 则对应的函数值y1、y2、y3的大小关系为( )
A.y1>y2>y3
B.y1<y2<y3
C.y2<y3<y1
D.y2>y3>y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖家开了甲、乙两个超市,两个超市在3月份的销售额均为a万元,在4月份和5月份这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%.
(1)5月份甲超市的销售额比乙超市多多少?
(2)如果a=250,x=2,那么5月份甲超市的销售额比乙超市多多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com