
【题目】如图,四边形OABC为直角梯形,已知AB∥OC,BC⊥OC,A点坐标为(3,4),AB=6.
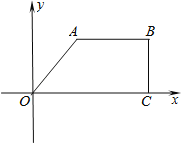
(1)求出直线OA的函数解析式;
(2)求出梯形OABC的周长;
(3)若直线l经过点D(3,0),且直线l将直角梯形OABC的面积分成相等的两部分,试求出直线l的函数解析式.
(4)若直线l经过点D(3,0),且直线l将直角梯形OABC的周长分为5:7两部分,试求出直线l的函数解析式.
【答案】(1)y=![]() x.(2)24.(3)y=
x.(2)24.(3)y=![]() x﹣8.(4)y=
x﹣8.(4)y=![]() x﹣2.
x﹣2.
【解析】解:(1)设OA的解析式为y=kx,
则3k=4,
∴k=![]() .
.
∴OA的解析式为y=![]() x.
x.
(2)如图,延长BA交y轴于点D.
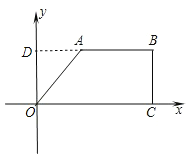
∵BA∥OC,
∴AD⊥y轴.且AD=3,OD=4.
∴AO=5,∴DB=3+6=9.
∴OC=9,又BC=OD=4.
∴COABC=OA+AB+BC+OC=5+6+4+9=24.
(3)如图
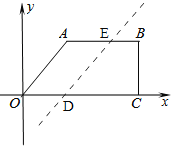
设点E的坐标为(a,4),
∴AE=a﹣3,
由(2)得AB=6,OC=9,BC=4,
∴S梯形OABC=![]() (AB+OC)×BC=
(AB+OC)×BC=![]() (6+9)×4=30,
(6+9)×4=30,
∵直线l经过点D(3,0),
∴OD=3,
∵直线l将直角梯形OABC的面积分成相等的两部分,
∴S梯形OAED=![]() S梯形OABC=
S梯形OABC=![]() ×30=15,
×30=15,
∴S梯形OAED=![]() (AE+OD)×BC=
(AE+OD)×BC=![]() ×(a﹣3+3)×4=15,
×(a﹣3+3)×4=15,
∴a=![]() ,
,
∴E(![]() ,4),
,4),
∵D(3,0),
∴直线解析式为y=![]() x﹣8.
x﹣8.
(4)∵COABC=24,故被l分成的两部分分别为10和14.
若l左边部分为10,则s=10﹣3=7,
∴P(5,4).
设PD为:y=mx+n,则![]() ,
,
∴![]() ,
,
∴y=2x﹣6;
若l左边部分为14,则s=14﹣3=11,
∴P(9,4).
∴![]() ,
,
∴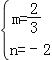 ,
,
∴y=![]() x﹣2.
x﹣2.


科目:初中数学 来源: 题型:
【题目】若a=-2×32,b=(-2×3)2,c=-(2×3)2,则下列大小关系中正确的是( )
A. a>b>c B. b>c>a C. c>a>b D. b>a>c
查看答案和解析>>
科目:初中数学 来源: 题型:
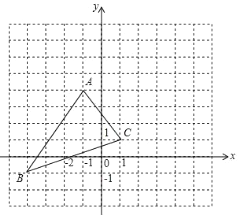
【题目】如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1( ),B1( ),C1( );
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个
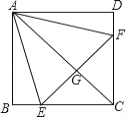
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
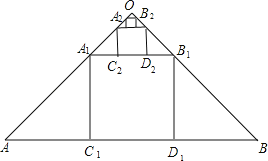
【题目】如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3;…;依次作下去,则第n个正方形AnBnCnDn的边长是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形的内部,有一个点到三角形三个顶点的距离相等,则这个点一定是三角形( )
A. 三条中线的交点
B. 三条角平分线的交点
C. 三条边的垂直平分线的交点
D. 三条高的交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com