Question

7．点P（t，0）是x轴上的动点，Q（0，2t）是y轴上的动点，若线段PQ与函数y=-|x|²+2|x|+3的图象只有一个公共点，则t的取值是$\frac{3}{2}$≤t＜3或t=$\frac{7}{2}$或t≤-3．

Answer 1

分析 先将函数y=-|x|²+2|x|+3的解析式去掉绝对值，变形为：y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3}&{（x≥0）}\\{-{x}^{2}-2x+3}&{（x＜0）}\end{array}\right.$，利用待定系数法求线段PQ的解析式，分情况进行讨论：①当线段PQ过（0，3）和过（3，0）时，计算出t的值，利用图形得出t的取值；②将y=-2x+2t代入y=-x²+2x+3（x≥0）中得，根据△=0得出t的值；③当线段PQ过B（-3，0），如图3，同理得出t的取值．

解答 解：函数y=-|x|²+2|x|+3的解析式可化为：
y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3}&{（x≥0）}\\{-{x}^{2}-2x+3}&{（x＜0）}\end{array}\right.$，
设线段PQ所在的直线的解析式为：y=kx+b，
将P（t，0）、Q（0，2t）代入得：$\left\{\begin{array}{l}{tk+b=0}\\{b=2t}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-2}\\{b=2t}\end{array}\right.$，
∴线段PQ所在的直线的解析式为：y=-2x+2t；
①当线段PQ过（0，3）时，即点Q与C重合，如图1，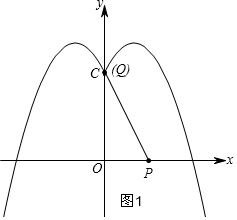

2t=3，
t=$\frac{3}{2}$，
∴当t=$\frac{3}{2}$时，线段PQ与函数y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3}&{（x≥0）}\\{-{x}^{2}-2x+3}&{（x＜0）}\end{array}\right.$只有一个公共点；
当线段PQ过（3，0）时，即点P与A（3，0）重合，如图2，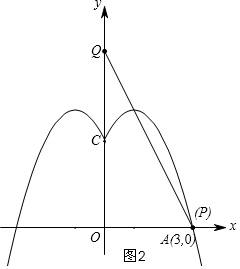

t=3，
此时线线段PQ与函数y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3}&{（x≥0）}\\{-{x}^{2}-2x+3}&{（x＜0）}\end{array}\right.$有两个公共点，
∴当$\frac{3}{2}$≤t＜3时，线段PQ与函数y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3}&{（x≥0）}\\{-{x}^{2}-2x+3}&{（x＜0）}\end{array}\right.$只有一个公共点；
②将y=-2x+2t代入y=-x²+2x+3（x≥0）中得，
-x²+2x+3=-2x+2t，
-x²+4x+3-2t=0，
△=16-4×（-1）×（3-2t）=28-8t=0，
t=$\frac{7}{2}$，
∴当t=$\frac{7}{2}$时，线段PQ与函数y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3}&{（x≥0）}\\{-{x}^{2}-2x+3}&{（x＜0）}\end{array}\right.$也只有一个公共点；
③当线段PQ过B（-3，0），如图3，即P与B（-3，0）重合，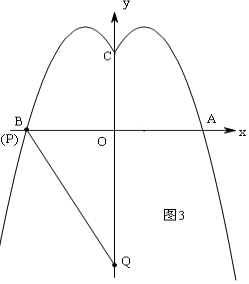

线段PQ只与y=-x²-2x+3（x＜0）有一个公共点，此时t=-3，
∴当t≤-3时，线段PQ与函数y=$\left\{\begin{array}{l}{-{x}^{2}+2x+3}&{（x≥0）}\\{-{x}^{2}-2x+3}&{（x＜0）}\end{array}\right.$也只有一个公共点；
综上所述，当线段PQ与函数y=-|x|²+2|x|+3只有一个公共点时，t的取值是$\frac{3}{2}$≤t＜3或t=$\frac{7}{2}$或t≤-3，
故答案为：$\frac{3}{2}$≤t＜3或t=$\frac{7}{2}$或t≤-3．

点评 本题考查了两个二次函数组合的复合函数的取值问题，利用数形结合的思想，从特殊位置着手，并注意是线段与函数有一个交点，采用了分类讨论的思想解决此题．