
【题目】如图,点A1、A2、A3…在直线y=x上,点C1,C2,C3…在直线y=2x上,以它们为顶点依次构造第一个正方形A1C1A2B1,第二个正方形A2C2A3B2…,若A2的横坐标是1,则B3的坐标是_____,第n个正方形的面积是_____.
[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/21/2208296361205760/2209339150704640/STEM/947823175bfc4b878475a9a15e16a258.png]
【答案】(4,2) 22n﹣4.
【解析】
由A2的横坐标是1,可得A2(1,1),利用两个函数解析式求出点C1、A1的坐标,得出A1C1的长度以及第1个正方形的面积,求出B1的坐标;然后再求出C2的坐标,得出第2个正方形的面积,求出B2的坐标;再求出B3、C3的坐标,得出第3个正方形的面积;从而得出规律即可得到第n个正方形的面积.
∵点A1、A2、A3…在直线y=x上,A2的横坐标是1,∴A2(1,1).
∵点C1,C2,C3…在直线y=2x上,∴C1 (![]() ,1),A1(
,1),A1(![]() ,
,![]() ),∴A1C1=1﹣
),∴A1C1=1﹣![]() =
=![]() ,B1(1,
,B1(1,![]() ),∴第1个正方形的面积为:(
),∴第1个正方形的面积为:(![]() )2;
)2;
∵C2(1,2),∴A2C2=2﹣1=1,B2(2,1),A3(2,2),∴第2个正方形的面积为:12;
∵C3(2,4),∴A3C3=4﹣2=2,B3(4,2),∴第3个正方形的面积为:22;
…
∴第n个正方形的面积为:(2n﹣2)2=22n﹣4.
故答案为:(4,2),22n﹣4.


科目:初中数学 来源: 题型:
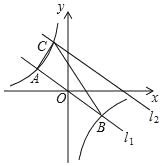
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2:
(1)求反比例函数的表达式;
(2)将直线l1:y=﹣![]() x向上平移后的直线l2与反比例函数y=
x向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
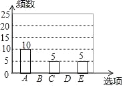
【题目】随着移动终端设备的升级换代,手机己经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天:B.学习:C.购物:D.游戏:E.其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):
选项 | 频数 | 百分比 |
A | 10 | m |
B | n | 20% |
C | 5 | 10% |
D | p | 40% |
E | 5 | 10% |
合计 | 100% |
根据以上信息解答下列问题:
(1)m= ,n= ,p= ;
(2)补全条形统计图;
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
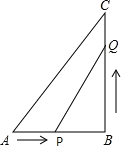
【题目】已知:如图所示.在△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在DE的位置上,测得BD长为0.5米,则梯子顶端A下落了( )米.

A. 0.5 B. 1 C. 1.5 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2014年湖南怀化10分)设m是不小于﹣1的实数,使得关于x的方程x2+2(m﹣2)x+m2﹣3m+3=0有两个不相等的实数根x 1,x2.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
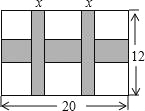
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com