
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
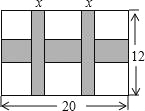
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
【答案】(1)y=﹣3x2+54x;(2)横彩条的宽度为3cm,竖彩条的宽度为2cm.
【解析】
试题分析:(1)由横、竖彩条的宽度比为3:2知横彩条的宽度为![]() xcm,根据“三条彩条面积=横彩条面积+2条竖彩条面积﹣横竖彩条重叠矩形的面积”,列出函数关系式化简即可;(2)根据“三条彩条所占面积是图案面积的
xcm,根据“三条彩条面积=横彩条面积+2条竖彩条面积﹣横竖彩条重叠矩形的面积”,列出函数关系式化简即可;(2)根据“三条彩条所占面积是图案面积的![]() ”,可列出关于x的一元二次方程,整理后求解即可.
”,可列出关于x的一元二次方程,整理后求解即可.
试题解析:(1)根据题意可知,横彩条的宽度为![]() xcm,
xcm,
∴y=20×![]() x+2×12x﹣2×
x+2×12x﹣2×![]() xx=﹣3x2+54x,
xx=﹣3x2+54x,
即y与x之间的函数关系式为y=﹣3x2+54x;
(2)根据题意,得:﹣3x2+54x=![]() ×20×12,
×20×12,
整理,得:x2﹣18x+32=0,
解得:x1=2,x2=16(舍),
∴![]() x=3,
x=3,
答:横彩条的宽度为3cm,竖彩条的宽度为2cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
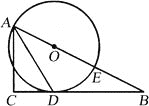
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(-2,0),点B(0,4),点E在OB上,且∠OAE=∠OBA.
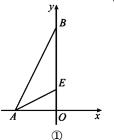
(1)如图①,求点E的坐标
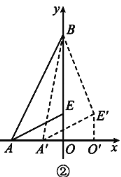
(2)如图②,将△AEO沿x轴向右平移得到△A′E′O′,连接A′B,BE′.
①设AA′=m,其中0<m<2,试用含m的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
②当A′B+BE′取得最小值时,求点E′的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图⊙O的内接△ABC中,外角∠ACF的角平分线与⊙O相交于D点,DP⊥AC,垂足为P,DH⊥BF,垂足为H.问:
(1)∠PDC与∠HDC是否相等,为什么?
(2)图中有哪几组相等的线段?
(3)当△ABC满足什么条件时,△CPD∽△CBA,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P0的坐标为(2,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图
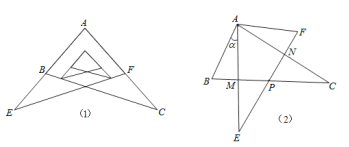
(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试航任务.某日航母在南海海域试航,如图,海中有一个小岛A,并测得该岛四周10海里内有暗礁,航母由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处,之后如果航母继续向东航行,途中会有触礁的危险吗?(参考数据:sin55°=0.8,cos55°=0.6,tan55°=1.4,sin25°=0.4,cos25°=0.9,tan25°=0.5)
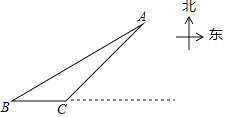
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com