
【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图
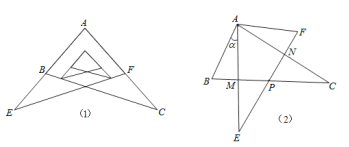
(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
【答案】解:(1)证明:∵用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),
∴AB=AF,∠BAM=∠FAN。
∵在△ABM和△AFN中,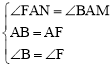 ,
,
∴△ABM≌△AFN(ASA)。
∴AM=AN。
(2)当旋转角α=30°时,四边形ABPF是菱形。理由如下:
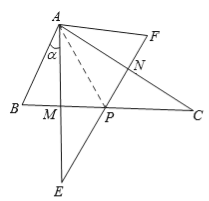
连接AP,
∵∠α=30°,∴∠FAN=30°。∴∠FAB=120°。
∵∠B=60°,∴AF∥BP。∴∠F=∠FPC=60°。
∴∠FPC=∠B=60°。∴AB∥FP。
∴四边形ABPF是平行四边形。
∵AB=AF,∴平行四边形ABPF是菱形。
【解析】(1)根据旋转的性质得出AB=AF,∠BAM=∠FAN,进而得出△ABM≌△AFN得出答案即可。
(2)利用旋转的性质得出∠FAB=120°,∠FPC=∠B=60°,即可得出四边形ABPF是平行四边形,再利用菱形的判定得出答案。


科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
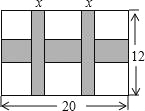
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
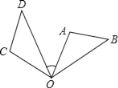
【题目】如图,将△OAB绕点O逆时针旋转80°得到△OCD,点A与点C是对应点.
(1)画出△OAB关于点O对称的图形(保留画图痕迹,不写画法);
(2)若∠A=110°,∠D=40°,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
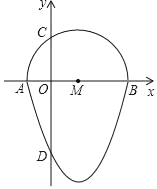
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y轴截得的线段CD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
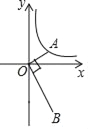
【题目】如图,已知点A是反比例函数y=![]() (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为( )
A. y=﹣![]() B. y=
B. y=![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
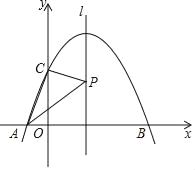
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,P为此抛物线对称轴l上任意一点,则△APC的周长的最小值是( )
x+2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,P为此抛物线对称轴l上任意一点,则△APC的周长的最小值是( )
A. 2![]() B. 3
B. 3![]() C. 5
C. 5![]() D.
D. ![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
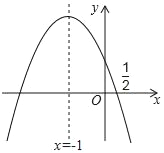
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com