
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1,且过点(![]() ,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
,0).有下列结论:①abc>0;②25a﹣10b+4c=0;③a﹣2b+4c=0;④a﹣b≥m(am﹣b);⑤3b+2c>0;其中所有正确的结论是_____(填写正确结论的序号).
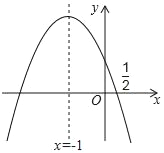
【答案】①②④
【解析】
首先根据抛物线![]() 的开口方向、对称轴及抛物线与y的交点可判断出a、b、c的符号,可确定①的正误;然后根据抛物线的对称轴为x=-1和抛物线与x轴的交点,可分别推得②③④⑤的正误.
的开口方向、对称轴及抛物线与y的交点可判断出a、b、c的符号,可确定①的正误;然后根据抛物线的对称轴为x=-1和抛物线与x轴的交点,可分别推得②③④⑤的正误.
①由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
②∵抛物线![]() 的对称轴是x=-1.且过点(
的对称轴是x=-1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为(![]() ,0),
,0),
当x=![]() 时,y=0,即
时,y=0,即![]() =0,
=0,
整理得:25a-10b+4c=0,故②正确;
③直线x=-1是抛物线![]() 的对称轴,所以
的对称轴,所以![]() =-1,
=-1,
解得b=2a,
∴a-2b+4c=a-4a+c=-3a+c.
∵a<0,
∴-3a>0.
∵c>0,
∴-3a+c>0.
即a-2b+4c>0,故③错误;
④∵x=-1时,函数值最大,
∴a-b+c![]() (m≠1),
(m≠1),
∴a-b![]() m(am-b),所以④正确;
m(am-b),所以④正确;
⑤∵x=1时,y<0,
∴a+b+c<0,
∵b=2a,a=![]()
∴![]() +b+c<0
+b+c<0
∴3b+2c<0,故⑤错误.
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图
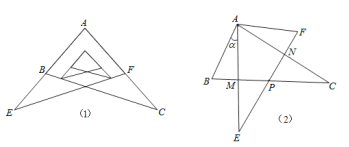
(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 0 |
| 2 |
| 0 | m | ﹣6 | ﹣ | … |
(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.
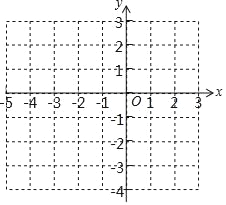
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为抛物线y=![]() x2上一动点.
x2上一动点.
(1)若抛物线y=![]() x2是由抛物线y=
x2是由抛物线y=![]() (x+2)2﹣1通过图象平移得到的,请写出平移的过程;
(x+2)2﹣1通过图象平移得到的,请写出平移的过程;
(2)若直线l经过y轴上一点N,且平行于x轴,点N的坐标为(0,﹣1),过点P作PM⊥l于M.
①问题探究:如图一,在对称轴上是否存在一定点F,使得PM=PF恒成立?若存在,求出点F的坐标:若不存在,请说明理由.
②问题解决:如图二,若点Q的坐标为(1.5),求QP+PF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试航任务.某日航母在南海海域试航,如图,海中有一个小岛A,并测得该岛四周10海里内有暗礁,航母由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处,之后如果航母继续向东航行,途中会有触礁的危险吗?(参考数据:sin55°=0.8,cos55°=0.6,tan55°=1.4,sin25°=0.4,cos25°=0.9,tan25°=0.5)
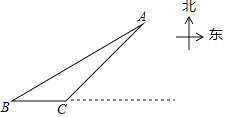
查看答案和解析>>
科目:初中数学 来源: 题型:
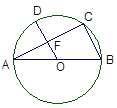
【题目】如图,A,B,C三点在⊙O上,且AB是⊙O的直径,半径OD⊥AC,垂足为F,若∠A=30,OF=3,则OA=_____,AC=_____,BC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的有 ( )个
①40°角为内角的两个等腰三角形必相似
②若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为750
③一组对边平行,另一组对边相等的四边形是平行四边形
④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2∶b2∶c2=2∶1∶1
⑤若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则此△为等腰直角三角形。
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com