
【题目】在平面直角坐标系中,已知点A(-2,0),点B(0,4),点E在OB上,且∠OAE=∠OBA.
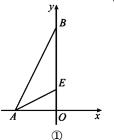
(1)如图①,求点E的坐标
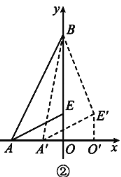
(2)如图②,将△AEO沿x轴向右平移得到△A′E′O′,连接A′B,BE′.
①设AA′=m,其中0<m<2,试用含m的式子表示A′B2+BE′2,并求出使A′B2+BE′2取得最小值时点E′的坐标;
②当A′B+BE′取得最小值时,求点E′的坐标(直接写出结果即可).
【答案】(1)(0,1)(2)①(1,1);②(![]() ,1).
,1).
【解析】
(1)根据相似三角形△OAE∽△OBA的对应边成比例得到![]() ,则易求OE=1,所以E(0,1);
,则易求OE=1,所以E(0,1);
(2)如图②,连接EE′.在Rt△A′BO中,勾股定理得到A′B2=(2-m)2+42=m2-4m+20,在Rt△BE′E中,利用勾股定理得到BE′2=E′E2+BE2=m2+9,则A′B2+BE′2=2m2-4m+29=2(m-1)2+27.所以由二次函数最值的求法知,当m=1即点E′的坐标是(1,1)时,A′B2+BE′2取得最小值.
(1)如图①,∵点A(-2,0),点B(0,4),
∴OA=2,OB=4.
∵∠OAE=∠0BA,∠EOA=∠AOB=90°,
∴△OAE∽△OBA,
∴![]() ,即
,即![]() ,
,
解得OE=1,
∴点E的坐标为(0,1);
(2)①如图②,连接EE′.
由题设知AA′=m(0<m<2),则A′O=2-m.
在Rt△A′BO中,由A′B2=A′O2+BO2,得A′B2=(2-m)2+42=m2-4m+20.
∵△A′E′O′是△AEO沿x轴向右平移得到的,
∴EE′∥AA′,且EE′=AA′.
∴∠BEE′=90°,EE′=m.
又∵BE=OB-OE=3,
∴在Rt△BE′E中,BE′2=E′E2+BE2=m2+9,
∴A′B2+BE′2=2m2-4m+29=2(m-1)2+27.
当m=1时,A′B2+BE′2可以取得最小值,此时,点E′的坐标是(1,1).
②如图②,过点A作AB′⊥x,并使AB′=BE=3.
易证△AB′A′≌△EBE′,
∴B′A′=BE′,
∴A′B+BE′=A′B+B′A′.
当点B、A′、B′在同一条直线上时,A′B+B′A′最小,即此时A′B+BE′取得最小值.
易证△AB′A′∽△OBA′,
∴![]() ,
,
∴![]() ,AO=2,
,AO=2,
∴AA′=![]() ×2=
×2=![]() ,
,
∴EE′=AA′=![]() ,
,
∴点E′的坐标是(![]() ,1).
,1).


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2-3x+2和一次函数y=-2x+4,把y=t(x2-3x+2)+(1-t)(-2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(-1,n),请完成下列任务:
(1)(尝试)
当t=2时,抛物线y=t(x2-3x+2)+(1-t)(-2x+4)的顶点坐标为________;
(2)判断点A是否在抛物线L上;
(3)求n的值.
(4)(发现)
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为________.
(5)(应用)
二次函数y=-3x2+5x+2是二次函数y=x23x+2和一次函数y=-2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
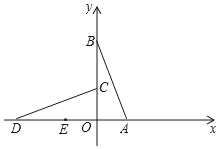
【题目】如图,已知点A(1,0),B(0,3),将△AOB绕点O逆时针旋转90°,得到△COD,设E为AD的中点.
(1)若F为CD上一动点,求出当△DEF与△COD相似时点F的坐标;
(2)过E作x轴的垂线l,在直线l上是否存在一点Q,使∠CQO=∠CDO?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“节能减排、绿色出行”的健康生活意识的普及,新能源汽车越来越多地走进百姓的生活.某汽车租赁公司拥有40辆电动汽车,据统计,当每辆车的日租金为120元时,可全部租出;当每辆车的日租金每增加5元时,未租出的车将增加1辆;该公司平均每日的各项支出共2100元.
(1)若某日共有x辆车未租出,则当日每辆车的日租金为 元;
(2)当每辆车的日租金为多少时,该汽车租赁公司日收益最大?最大日收益是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
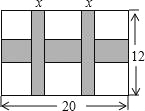
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
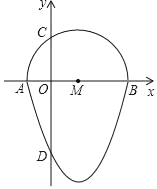
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2﹣6x﹣16,AB为半圆的直径,则这个“果圆”被y轴截得的线段CD的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com