【题目】随着“节能减排、绿色出行”的健康生活意识的普及，新能源汽车越来越多地走进百姓的生活．某汽车租赁公司拥有40辆电动汽车，据统计，当每辆车的日租金为120元时，可全部租出；当每辆车的日租金每增加5元时，未租出的车将增加1辆；该公司平均每日的各项支出共2100元．
（1）若某日共有x辆车未租出，则当日每辆车的日租金为 元；
（2）当每辆车的日租金为多少时，该汽车租赁公司日收益最大？最大日收益是多少？
科目：初中数学 来源： 题型：
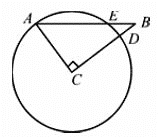
【题目】如图，△ABC中，∠C=Rt∠，AC=6，BC=8，以点C为圆心，CA为半径的圆与AB，BC分别交于点E，D，则BE的长为( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，网格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC是格点三角形．在建立平面直角坐标系后，点B的坐标为(－1，－1)．
(1)把△ABC向下平移5格后得到△A1B1C1，写出点A1，B1，C1的坐标，并画出△A1B1C1；
(2)把△ABC绕点O按顺时针方向旋转180°后得到△A2B2C2，写出点A2，B2，C2的坐标，并画出△A2B2C2；
(3)把△ABC以点O为位似中心放大得到△A3B3C3，使放大前后对应线段的比为1∶2，写出点A3，B3，C3的坐标，并画出△A3B3C3.
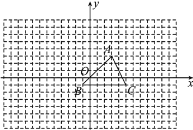
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某足球运动员站在点O处练习射门，将足球从离地面0.5m的A处正对球门踢出(点A在y轴上)，足球的飞行高度y(单位：m)与飞行时间t(单位：s)之间满足函数关系y＝at2＋5t＋c，已知足球飞行0.8s时，离地面的高度为3.5m.
(1)足球飞行的时间是多少时，足球离地面最高？最大高度是多少？
(2)若足球飞行的水平距离x(单位：m)与飞行时间t(单位：s)之间具有函数关系x＝10t，已知球门的高度为2.44m，如果该运动员正对球门射门时，离球门的水平距离为28m，他能否将球直接射入球门？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5
的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元：
（1）求出y与x的函数关系式.(纯利润=总收入-总支出)
（2）当y=106000时,求该厂在这个月中生产产品的件数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知点A(－2，0)，点B(0，4)，点E在OB上，且∠OAE＝∠OBA.
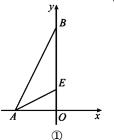
(1)如图①，求点E的坐标
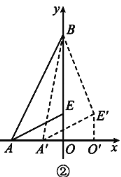
(2)如图②，将△AEO沿x轴向右平移得到△A′E′O′，连接A′B，BE′.
①设AA′＝m，其中0<m<2，试用含m的式子表示A′B2＋BE′2，并求出使A′B2＋BE′2取得最小值时点E′的坐标；
②当A′B＋BE′取得最小值时，求点E′的坐标(直接写出结果即可).
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知点P0的坐标为（2，0），将点P0绕着原点O按逆时针方向旋转60°得点P1，延长OP1到点P2，使OP2=2OP1，再将点P2绕着原点O按逆时针方向旋转60°得点P3，则点P3的坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P为抛物线y=
x2上一动点．
（1）若抛物线y=x2是由抛物线y=（x+2）2﹣1通过图象平移得到的，请写出平移的过程；
（2）若直线l经过y轴上一点N，且平行于x轴，点N的坐标为（0，﹣1），过点P作PM⊥l于M．
①问题探究：如图一，在对称轴上是否存在一定点F，使得PM=PF恒成立？若存在，求出点F的坐标：若不存在，请说明理由．
②问题解决：如图二，若点Q的坐标为（1.5），求QP+PF的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
