
【题目】某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5![]() 的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1
的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1![]() 污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:
污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:
(1)求出y与x的函数关系式.(纯利润=总收入-总支出)
(2)当y=106000时,求该厂在这个月中生产产品的件数.
【答案】(1)y=19x-8000(x>0且x是整数) (2)6000件
【解析】
(1)本题的等量关系是:纯利润=产品的出厂单价×产品的数量-产品的成本价×产品的数量-生产过程中的污水处理费-排污设备的损耗,可根据此等量关系来列出总利润与产品数量之间的函数关系式;
(2)根据(1)中得出的式子,将y的值代入其中,求出x即可.
(1)依题意得:y=80x-60x-0.5x2-8000,
化简得:y=19x-8000,
∴所求的函数关系式为y=19x-8000.(x>0且x是整数)
(2)当y=106000时,代入得:106000=19x-8000,
解得x=6000,
∴这个月该厂生产产品6000件.


科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OFDE=OE2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
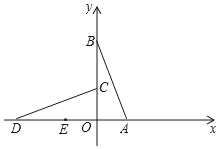
【题目】如图,已知点A(1,0),B(0,3),将△AOB绕点O逆时针旋转90°,得到△COD,设E为AD的中点.
(1)若F为CD上一动点,求出当△DEF与△COD相似时点F的坐标;
(2)过E作x轴的垂线l,在直线l上是否存在一点Q,使∠CQO=∠CDO?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
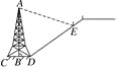
【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=24 m,小明和小华的身高都是1.6 m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2 m和1 m,那么塔高AB为________ m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“节能减排、绿色出行”的健康生活意识的普及,新能源汽车越来越多地走进百姓的生活.某汽车租赁公司拥有40辆电动汽车,据统计,当每辆车的日租金为120元时,可全部租出;当每辆车的日租金每增加5元时,未租出的车将增加1辆;该公司平均每日的各项支出共2100元.
(1)若某日共有x辆车未租出,则当日每辆车的日租金为 元;
(2)当每辆车的日租金为多少时,该汽车租赁公司日收益最大?最大日收益是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用![]() 表示不大于
表示不大于![]() 的最大整数,例如:
的最大整数,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整数,例如:
的最小整数,例如:![]() ,
,![]() ,
,![]() .解决下列问题:
.解决下列问题:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,则
=2,则![]() 的取值范围是 ;若
的取值范围是 ;若![]() =-1,则
=-1,则![]() 的取值范围是 ;
的取值范围是 ;
(3)已知![]() ,
,![]() 满足方程组
满足方程组![]() ,求
,求![]() ,
,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
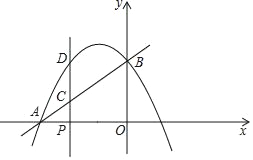
【题目】如图,在直角坐标系中,O是坐标原点,直线AB交x轴于点A(﹣4,0),交y轴于点B,抛物线y=ax2+2ax+3(a≠0)经过A,B两点.P是线段AO上的一动点,过点P作PC⊥x轴交直线AB于点C,交抛物线于点D.
(1)求a及AB的长.
(2)连结PB,若tan∠ABP=![]() ,求点P的坐标.
,求点P的坐标.
(3)连结BD,以BD为边作正方形BDEF,是否存在点P使点E恰好落在抛物线的对称轴上?若存在,请求出点P的坐标;若不存在,请说明理由.
(4)连结OC,若S△BDC:S△OBC=1:2,将线段BD绕点D按顺时针方向旋转,得到DB′.则在旋转的过程中,当点A,B到直线DB′的距离和最大时,请直接写出点B′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com