
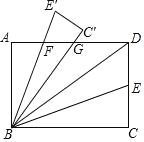
【题目】如图,矩形ABCD中,AB=3,AD=4,连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当线段BE′和线段BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
先在Rt△ABD中利用勾股定理求出BD=5,在Rt△ABF中利用勾股定理求出BF=![]() ,则AF=4-
,则AF=4-![]() =
=![]() .再过G作GH∥BF,交BD于H,证明GH=GD,BH=GH,设DG=GH=BH=x,则FG=FD-GD=
.再过G作GH∥BF,交BD于H,证明GH=GD,BH=GH,设DG=GH=BH=x,则FG=FD-GD=![]() -x,HD=5-x,由GH∥FB,得出
-x,HD=5-x,由GH∥FB,得出![]() =
=![]() ,即可求解.
,即可求解.
解:在Rt△ABD中,∵∠A=90°,AB=3,AD=4,
∴BD=5,
在Rt△ABF中,∵∠A=90°,AB=3,AF=4-DF=4-BF,
∴BF2=32+(4-BF)2,
解得BF=![]() ,
,
∴AF=4-![]() =
=![]() .
.
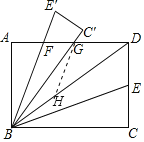
过G作GH∥BF,交BD于H,
∴∠FBD=∠GHD,∠BGH=∠FBG,
∵FB=FD,
∴∠FBD=∠FDB,
∴∠FDB=∠GHD,
∴GH=GD,
∵∠FBG=∠EBC=![]() ∠DBC=
∠DBC=![]() ∠ADB=
∠ADB=![]() ∠FBD,
∠FBD,
又∵∠FBG=∠BGH,∠FBG=∠GBH,
∴BH=GH,
设DG=GH=BH=x,则FG=FD-GD=![]() -x,HD=5-x,
-x,HD=5-x,
∵GH∥FB,
∴ ![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得x=![]() .
.
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,有三条线段![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() .点
.点![]() 和点
和点![]() 分别为
分别为![]() 上的两个动点,且
上的两个动点,且![]() .
.
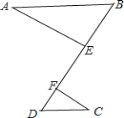
![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 时,求
时,求![]() 的长度;
的长度;
![]() 在以上
在以上![]() 个问题的解题过程中,概括(或者描述)你所用到数学基本知识(定义、定理等)或者是利用的数学思想方法.(共写出
个问题的解题过程中,概括(或者描述)你所用到数学基本知识(定义、定理等)或者是利用的数学思想方法.(共写出![]() 点即可)
点即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 与
与![]() 成正比例,
成正比例,![]() ,
,![]() 为常数
为常数
(1)试说明:![]() 是
是![]() 的一次函数;
的一次函数;
(2)若![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,求函数关系式;
,求函数关系式;
(3)将(2)中所得的函数图象平移,使它过点![]() ,求平移后的直线的解析式.
,求平移后的直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
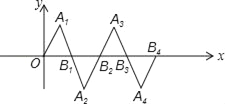
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若A的对应点A2的坐标为(0,4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8cm,BC=12cm,点P从点B出发,以2cm/秒的速度沿BC向终点C运动,设点P的运动时间为t秒.
(1)当t=3时,求证:△ABP≌△DCP.
(2)当点P从点B开始运动的同时,点Q从点C出发,以v cm/秒的速度沿CD向终点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,先将这50台联合收割机派往A、B两地区收割小麦,其中30台派往A地区,20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见表:
每台甲型收割机的租金 | 每台乙型收割机的租金 | |
A地区 | 1800 | 1600 |
B地区 | 1600 | 1200 |
(1)设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y(元),求y与x间的函数关系式,并写出x的取值范围;
(2)若使农机租赁公司这50台联合收割机一天获得的租金总额不低于79 600元,说明有多少种分配方案,并将各种方案设计出来;
(3)如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提一条合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com