
【题目】如图,在矩形ABCD中,AB=8cm,BC=12cm,点P从点B出发,以2cm/秒的速度沿BC向终点C运动,设点P的运动时间为t秒.
(1)当t=3时,求证:△ABP≌△DCP.
(2)当点P从点B开始运动的同时,点Q从点C出发,以v cm/秒的速度沿CD向终点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.

【答案】(1)证明见解析;(2)存在;v=2或v=![]() .
.
【解析】
(1)根据全等三角形的判定即可解答;
(2)此题主要分两种情况①△ABP≌△PCQ得到BP=CQ,AB=PC,②△ABP≌△QCP得到BA=CQ,PB=PC,然后分别计算出t的值,进而得到v的值.
证明:(1)当t=3时,BP=2×3=6,
∴PC=12﹣6=6,
∴BP=PC,
在矩形ABCD中,AB=CD,∠B=∠C=90°,
在△ABP与△DCP中
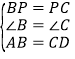 ,
,
∴△ABP≌△DCP.
(2)①当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=8,
∴PC=8,
∴BP=12﹣8=4,
∴2t=4,
解得:y=2,
∴CQ=BP=4,
v×2=4,
解得:v=2;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∵PB=PC,
∴BP=PC=6,
∴2t=6,解得:t=3,
∴CQ=AB=8,v×3=8,
解得:v=![]() ,
,
综上所述,当v=2或v=![]() 时,△ABP与△PQC全等.
时,△ABP与△PQC全等.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】某部门组织调运一批物资,一运送物资车开往距离出发地180千米的目的地,出发第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地.设原计划速度为x千米/小时,则方程可列为( )
A. ![]() +
+![]() =
=![]() B.
B. ![]() -
-![]() =
=![]() C.
C. ![]() +1=
+1=![]() ﹣
﹣![]() D.
D. ![]() +1=
+1=![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是( )

A. 45.2分钟 B. 48分钟 C. 46分钟 D. 33分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线![]() 上,转轴
上,转轴![]() 到地面的距离
到地面的距离![]() ,小亮在荡秋千过程中,当秋千摆动到最高点
,小亮在荡秋千过程中,当秋千摆动到最高点![]() 时,测得点
时,测得点![]() 到
到![]() 的距离
的距离![]() ,点
,点![]() 到地面的距离
到地面的距离![]() :当他从
:当他从![]() 处摆动到
处摆动到![]() 处时,有
处时,有![]() .
.
(1)求![]() 到
到![]() 的距离;
的距离;
(2)求![]() 到地面的距离.
到地面的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,AD=4,连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当线段BE′和线段BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为( )
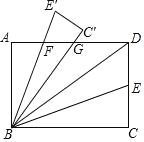
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°,BD、CE分别是△ABC、△BCD的角平分线.则图中的等腰三角形有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,公路上有![]() 三个车站,一辆汽车从
三个车站,一辆汽车从![]() 站以速度
站以速度![]() 匀速驶向
匀速驶向![]() 站,到达
站,到达![]() 站后不停留,以速度
站后不停留,以速度![]() 匀速驶向
匀速驶向![]() 站,汽车行驶路程
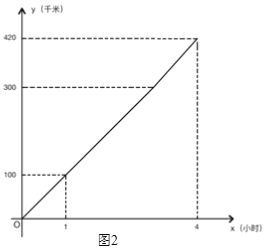
站,汽车行驶路程![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数图象如图2所示.
(小时)之间的函数图象如图2所示.
(1)求![]() 与
与![]() 之间的函数关系式及自变量的取值范围.
之间的函数关系式及自变量的取值范围.
(2)汽车距离C站20千米时已行驶了多少时间?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料:我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、十字相乘法等等,其中十字相乘法在高中应用较多.
十字相乘法:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如图),如:将式子![]() 和
和![]() 分解因式,如图:
分解因式,如图:
![]() ;
;
![]() .
.
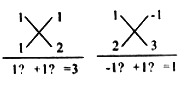
请你仿照以上方法,探索解决下列问题:
(1)分解因式:![]() ;
;
(2)分解因式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BE平分∠ABC,DE∥BC.
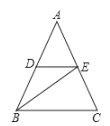
(1)试猜想△BDE的形状,并说明理由;
(2)若∠A=35°,∠C=70°,求∠BDE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com