Question

19．如图，已知?ABCD的面积是S，依次连接?ABCD各边中点构成第二个平行四边形?EFGH，再依次连接第二个平行四边形各边中点构成第三个平行四边形，…以此类推，则第109个平行四边形的面积为$\frac{1}{{2}^{108}}$S．

Answer 1

分析 连接EG，HF，相交于点O，有平行四边形的判定方法和平行四边形的性质：被对角线分的两个三角形的面积相等，可得新生成的平行四边形和前一个四边形的面积之间的关系，得出规律，按此规律即可求出第109个平行四边形的面积．

解答 解：连接EG，HF，相交于点O，
∵四边形ABCD是平行四边形，
∴AD∥BC，AD=BC，
∵H和F为中点，
∴AH=BF，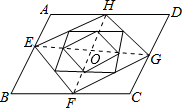
∴四边形ABFH为平行四边形，
∴AE∥HO，
同理可证：EO∥AH，
∴四边形AEOH是平行四边形，
∵EH是对角线，
∴S_△AEH=S_△EOH=$\frac{1}{2}$S_AEOH，
同理可得：S_△EOF=S_△BEF=$\frac{1}{2}$S_{四边形EBFO}，S_△CFG=S_△FOG=$\frac{1}{2}$S_{四边形FOGC}，S_△DHG=S_△HOG=$\frac{1}{2}$S_{四边形HOGD}，
∴S_{四边形EFGH}=$\frac{1}{2}$S_{四边形ABCD}=$\frac{1}{2}$S，
∴第三个平行四边形的面积为$\frac{1}{2}$×$\frac{1}{2}$S，
以此类推，可知每一个新生成的平行四边形都为前一个平行四边形面积的$\frac{1}{2}$，
∴第109个平行四边形的面积=$\frac{1}{{2}^{108}}$S．
故答案为$\frac{1}{{2}^{108}}$S．

点评 本题考查了平行四边形的判定和平行四边形的性质，解题的关键是找到规律，根据规律求出第109个平行四边形的面积．